問題
次の文章は,直流他励電動機の制御に関する記述である。ただし,鉄心の磁気飽和と電機子反作用は無視でき,また,電機子抵抗による電圧降下は小さいものとする。
a.他励電動機は,\fbox{(ア)}と\fbox{(イ)}を独立した電源で制御できる。磁束は\fbox{(ア)}に比例する。
b.磁束一定の条件で\fbox{(イ)}を増減すれば,\fbox{(イ)}に比例するトルクを制御できる。
c.磁束一定の条件で\fbox{(ウ)}を増減すれば,\fbox{(ウ)}に比例する回転数を制御できる。
d.\fbox{(ウ)}一定の条件で磁束を増減すれば,ほぼ磁束に反比例する回転数を制御できる。回転数の\fbox{(エ)}のために\fbox{(ア)}を弱める制御がある。
このように広い速度範囲で速度とトルクを制御できるので,直流他励電動機は圧延機の駆動などに広く使われてきた。
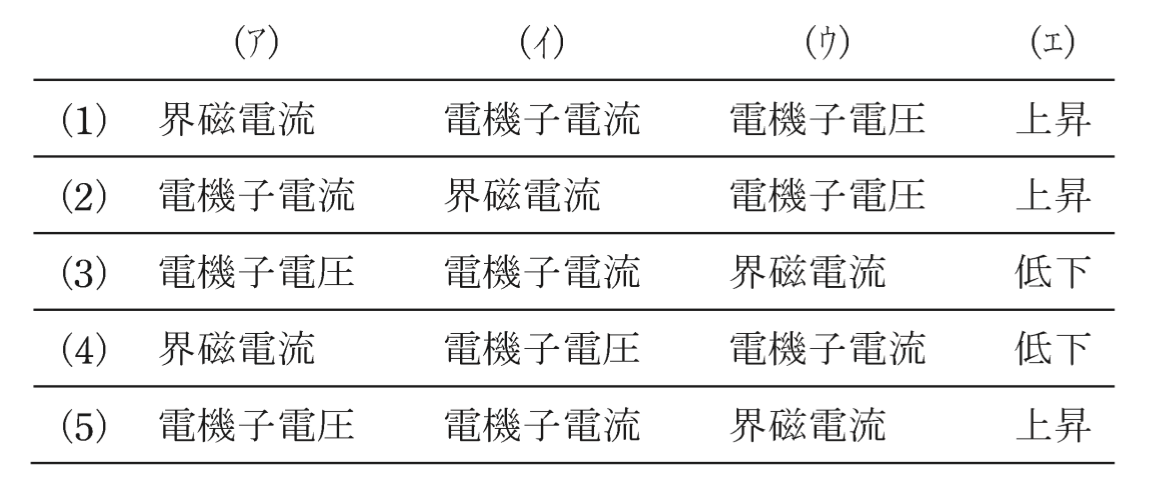
上記の記述中の空白箇所(ア)〜(エ)に当てはまる組合せとして,正しいものを次の(1)〜(5)のうちから一つ選べ。
解説
電流が流れている導体を磁界の中に置くと,フレミングの左手の法則により,導体は力を受けます。直流電動機はこの原理を利用した電動機です。導体が受ける力の大きさは,電動機の磁極の磁界の大きさと,電動機の導体に流れる電流の大きさに比例するため,これらの大きさを変化させることで,電動機を制御することができます。
直流電動機では,磁極で磁界を発生させる回路を界磁回路,力を受ける導体の回路を電機子回路と呼びますが,界磁回路のための電源と電機子回路のための電源をそれぞれ別々の電源としたものを,他励電動機と呼びます。
「他励」について
「他励」の「励」とは,励磁の略です。励磁とはコイルに電流を流して磁界を発生させることです。「他」は文字通り「ほか」ということですので,電機子回路とは別のという意味です。
(ア)
最初の説明のとおり,他励電動機は界磁回路と電機子回路がそれぞれ別々の電源に接続されています。したがって,それぞれの回路に流れる電流の大きさは,それぞれの電源の電圧を変えることで変化させることができます。界磁回路に流れる電流は,界磁電流,電機子回路に流れる電流は電機子電流です。磁束に関する電流は界磁電流であるため,「界磁電流」が適切な解答です。
(イ)
先の問題から,解答は「電機子電流」になります。
直流電動機はフレミングの左手の法則により動作しますが,直流電動機の電機子回路の導体1本が受ける力の大きさを F [N],導体1本に流れる電流を I [A],導体の長さを l [m],磁束密度を B [T]とすると,
F = IBl
と表すことができます。電動機のトルクは,電動機の軸に発生するねじり力であり,その大きさを T [N・m]とすると,トルクの定義のとおりその大きさは,軸から力の生じる導体までの距離 r [m]と導体に生じる力の大きさ F [N]の積で表されますので,
T= Fr = IBlr
となります。ここで, l と r は電動機の形状により決まるものであり,電動機の動作中に変化させることができるのはI と B です。
問題では磁束を一定としていますので,発生するトルクは上式のとおり電機子電流Iに比例します。
(ウ)
今度は電動機の回転数制御に関しての問題です。この問題は,他励電動機の回転数がどのような式で表されるのかを知っていないと,正しく解答することが出来ません。
他励電動機の回転数を式で表現するため,以下の等価回路を使います。

上図の左側は他励電動機の模式図です。電機子が回転することにより発生する電圧をE,電機子回路の抵抗をR_aとしています。また電機子回路に接続する電源の電圧をV_a,界磁回路に接続する電源の電圧をV_f,電機子に流れる電流をI_aとしています。
右側は電機子回路の部分を等価回路で表現したものです。この等価回路において,電動機の回転数が関係するのは,電機子回路が回転することによって発生する電圧Eの大きさです。
電機子回路に電圧が発生する理由は,導体が磁束の中を動くと電圧が発生するという,フレミングの右手の法則です。磁束の中を動く導体は電機子回路の導体になりますが,この回路の1本の導体に発生する電圧の大きさをE_1[V],1本の導体の移動速度をv[m/s],導体1本の導体の長さをl[m],磁束密度B [T]とすると,フレミングの右手の法則より,
E_1 = vBl
と表すことができます。
導体は回転しているため,円上を移動するように動きますが,導体の移動速度vは,その円の接線方向の速度です。この速度は回転する速度,回転数 n [rpm]に比例します。導体の長さlは,電動機の物理的な構造により決まる値であるため,1本の導体に発生する電圧の大きさをE_1とすると,E_1は回転数nと磁束密度Bに比例します。
電機子の内部では,電機子の導体をいくつか直列,あるいは並列に接続しているため,電機子回路として発生する電圧EはE_1に比例し,Eも回転数nと磁束密度Bに比例することになります。その比例定数をKとすると,
E = KBn
と表すことができます。
ここで,等価回路に戻ります。等価回路より,電動機の電機子回路の端子電圧V_aと電機子回路で発生する電圧Eとの関係を書くと,
V_a = E + R_aI_a
となります。この式に先ほど求めた回転数と発生電圧との関係式を代入すると,
V_a = KBn + R_aI_a
n = \dfrac{V_a - R_aI_a}{KB}
となり,回転数nに関する式が求まります。
問題では磁束を一定としているため,電機子電圧V_aを変化させることで,回転数を制御することができます。
問題文の(ウ)に「電機子電圧」を入れて問題文を読むと,「電機子電圧に比例する回転数を制御できる」となりますが,回転数を表す式には電機子電流も含まれており,電機子電圧を変化させると,電機子電流I_aも変化するため,回転数は電機子電圧に比例しないように見えます。
ただ,一般的にはR_aは小さな値であるため,R_aI_aの値も小さくなり,回転数はほぼ電機子電圧V_aに比例すると言えると思います。
なお,回転数を表す式において,磁束密度Bを使わずに,磁束\Phiで表現することも多いですが,\PhiはBに磁束が発生する磁極の面積をかけることで求まります。Bで表現するか\Phiで表現するかは,この件については本質的なところではなく,式を見るうえでは界磁回路で発生する磁界だと理解していればよいかと思います。
(エ)
回転数の式をみると,磁束の大きさは分数の分母にあるため,回転数と磁束は反比例の関係にあります。(ア)は界磁電流でしたので,界磁電流を弱めると磁束も弱まり,その結果回転数は上昇することになります。
解答
(1)