問題
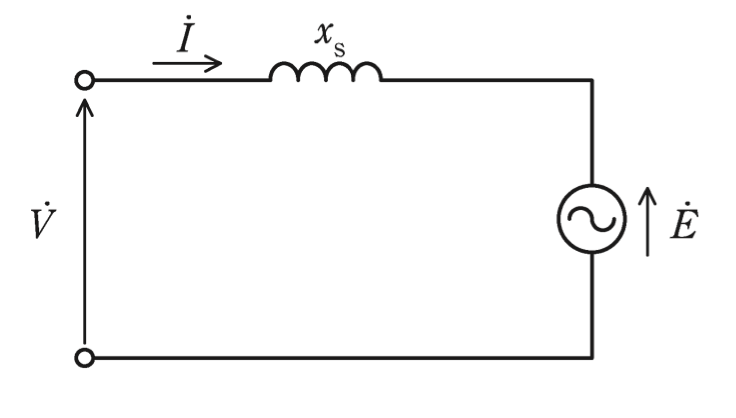
図はある三相同期電動機の1相分の等価回路である。ただし,電機子巻線抵抗は無視している。相電圧\dot{V}の大きさはV=200V,同期リアクタンスはx_s = 8 Ωである。この電動機を運転して力率が1になるように界磁電流を調整したところ,電機子電流\dot{I}の大きさIが10Aになった。このときの誘導起電力Eの値[V]として,最も近いものを次の(1)〜(5)のうちから一つ選べ。
(1)120 (2)140 (3)183 (4)215 (5)280
解説
問題の回路図より,相電圧\dot{V}と誘導起電力Eとの関係を,電機子電流\dot{I}を用いて表現すると,以下のとおりとなります。
\dot{V} = jx_s \dot{I} + \dot{E}
問題文に力率が1になるように界磁電流を調整したとあるため,相電圧\dot{V}と電機子電流\dot{I}は同位相になります。
上記の式から,電動機の相電圧\dot{V}は,誘導起電力\dot{E}と電機子電流\dot{I}を90°回転させたもの,すなわちj\dot{I}にx_sをかけたものとのベクトル和になっています。
これらをベクトル図で表すと以下のようになります。
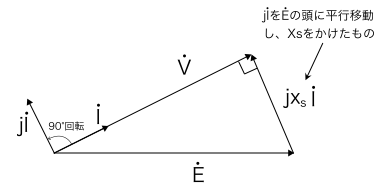
\dot{V}の大きさは,問題文より200,jx_s\dot{I}の大きさは,
\left | jx_s\dot{I} \right | = 8 \times 10 = 80
であるので,ベクトル図より,誘導起電力\dot{E}の大きさは,
\left | \dot{E} \right | = \sqrt{\left | \dot{V} \right |^2 + \left | jx_s \dot{I} \right |^2 } = \sqrt{200^2 + 80^2} \fallingdotseq 215 [V]
となります。
解答
(4)