問題
図のように，紙面に平行な平面内の平等電界E[V/m]中で2Cの点電荷を点Aから点Bまで移動させ，さらに点Bから点Cまで移動させた。この移動に，外力による仕事W=14Jを要した。点Aの電位に対する点Bの電位V_{BA}[V]の値として，最も近いものを次の（1）〜（5）のうちから一つ選べ。
ただし，点電荷の移動はゆっくりであり，点電荷の移動によってこの平等電界は乱れないものとする。
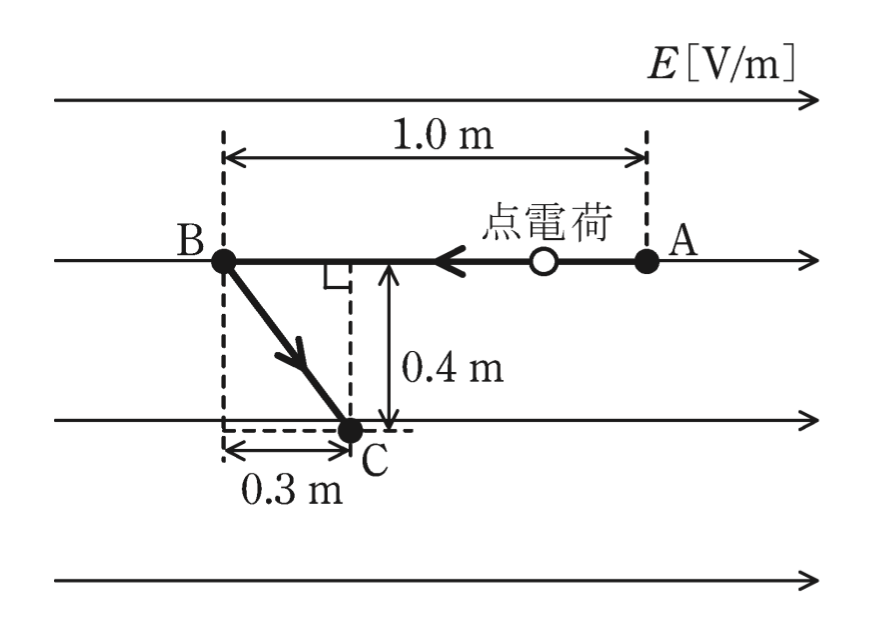
（1）5 （2）7 （3）10 （4）14 （5）20
解説
電界に置かれた点電荷には力が作用するため，それを動かすためには外部の力を必要とします。外部の力をF[N]，移動距離をd[m]，その仕事量をW[J]とすると，仕事量は力と移動距離の積であるため，以下のように表されます。
W=Fd
実際に電界の中で電荷を動かそうとすると，電荷が電界から受ける力よりも少しでも大きな力でないと，電荷を動かすことはできません。しかしながら，問題の仮定が「点電荷の移動はゆっくりであり，点電荷の移動によってこの平等電界は乱れない」となっていますので，このほんの少しだけ大きい力のほんの少し分の力はほぼ0に近いと考えてもよく，その場合は電荷を動かすための力と電荷が電界から受ける力の大きさは等しいと考えてよくなります。したがって，計算では電荷を動かすための力の大きさと電荷が電界から受ける力の大きさは等しいとして計算していきます。
問題ではAからBに動かしたあと，BからCに電荷を移動させていますので，それぞれの移動に必要な仕事量を求めて行きます。
step
1AからBに電荷を動かすために必要な仕事量
AからBに電荷を動かすための力は，電界から受ける力と等しいとして計算していきますが，電界はEであるため，その力をF_1[N]，電荷の電荷量をQ[C]とすると，
F_1=QE
となります。
移動距離をd_1[m]，電荷を動かすための仕事量をW_1[J]とすると，
W_1=F_1d_1=QEd_1
電荷量は2C，移動距離は1mであるので，
W_1=2E
となります。
step
2BからCに電荷を動かすために必要な仕事量
BからCは斜め方向の移動のため，複雑に見えますが，仕事量は力が0であれば発生しません。下図に示すように，電荷が電界から受ける力は電界の方向のみであり，電界に垂直な方向には力が発生しません。
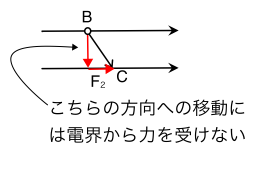
BからCへの電荷の移動は，まず電界の垂直方向に電荷を移動した後，電界の方向に沿って電荷を動かすと考えると，垂直方向の移動に必要な力は無く，電界の方向への移動に必要な力の仕事量のみを考えればよいことになります。電界の方向への移動に必要な力をF_2、電荷が力を受ける方向の移動距離をd_2とし，その仕事量をW_2とすると，
W_2=F_2d_2
となります。
F_2はF_1とは向きが逆で大きさは同じであるため，
F_2=-F_1=-QE
となります。これをW_2の式に代入すると，
W_2=-QEd_2
Qは２C,d_2は0.3mであるため，
W_2=-2E0.3=-0.6E
となります。
別解
下図のとおり，BからCへ斜めに移動する力の成分とその移動距離によっても仕事量を求めることは可能です。
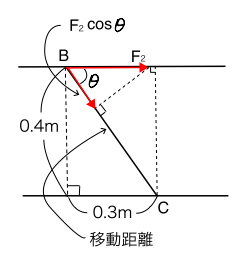BからCへの方向の力の成分は，
F_2 cos \theta
であり，移動距離は
\sqrt{0.3^2+0.4^2}=0.5
です。cos \thetaは図から
cos \theta =\dfrac{0.3}{0.5}
であるので，求める仕事量は
F_2 cos \theta 0.5=F_2 \dfrac{0.3}{0.5} 0.5=F_2 0.3=-QE0.3=-2E0.3=-0.6E
となり，先ほど求めた値と同じになります。
こちらの方が理解はしやすいですが，計算量が多くなり時間が掛かるため，問題数の多い電験の問題を解くには，最初の方法で簡単に求めた方がよいかと思います。
step
3全体の仕事量
全体の仕事量は，W_1とW_2の和であり，
W_1+W_2=2E−0.6E=1.4E
となります。この大きさが問題より14Jであるので，
1.4E=14
となり，これより電界Eを求めると，
E=10
となります。
解答
（3）
