問題
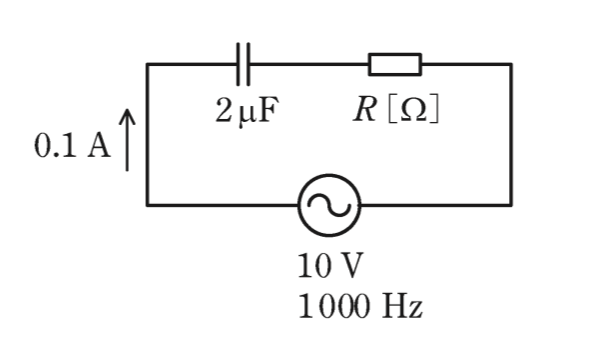
図のように,静電容量2μFのコンデンサ,R[Ω]の抵抗を直列に接続した。この回路に,正弦波交流電圧10V,周波数1 000 Hzを加えたところ,電流0.1Aが流れた。抵抗Rの値[Ω]として,最も近いものを次の(1)〜(5)のうちから一つ選べ。
(1)4.50 (2)20.4 (3)30.3 (4)60.5 (5)79.6
解説
回路に流れる電流とインピーダンスとの関係式を求め,与えられている値を代入して求めていきます。
コンデンサと抵抗は直列に接続されているため,コンデンサの容量をC[F],回路の角周波数を\omega[rad/s]とすると,回路のインピーダンスは
R+\dfrac{1}{j \omega C}
となります。大きさで表すと
\sqrt{R^2+{\left( \dfrac{1}{\omega C}\right)}^2}
となります。
電源の大きさをE[V],回路に流れる電流の大きさをI[A]とすると,
I=\dfrac{E}{\sqrt{R^2+ \left( \dfrac{1}{\omega C}\right)^2}}
となります。
回路の周波数をf[Hz]とすると,\omega = 2 \pi fであるので,上記式に与えられた値を代入すると,
0.1=\dfrac{10}{\sqrt{R^2+ \left( \dfrac{1}{2 \pi 1000 \times 2 \times 10^{-6}}\right)^2}}
となります。この式からRは,
10=0.1 \sqrt{R^2+ \left( \dfrac{1}{2 \pi 1000 \times 2 \times 10^{-6}}\right)^2}
10000=R^2+ \left( \dfrac{1}{4 \pi 10^{-3}}\right)^2
R^2=10000- \left( \dfrac{10^3}{4 \pi}\right)^2 = 10000 - \dfrac{1000000}{16 \pi ^2}
R^2 \fallingdotseq 3661.0
R \fallingdotseq 60.5
と求まります。なお,この計算では,\piを3.14としています。
解答
(4)