問題
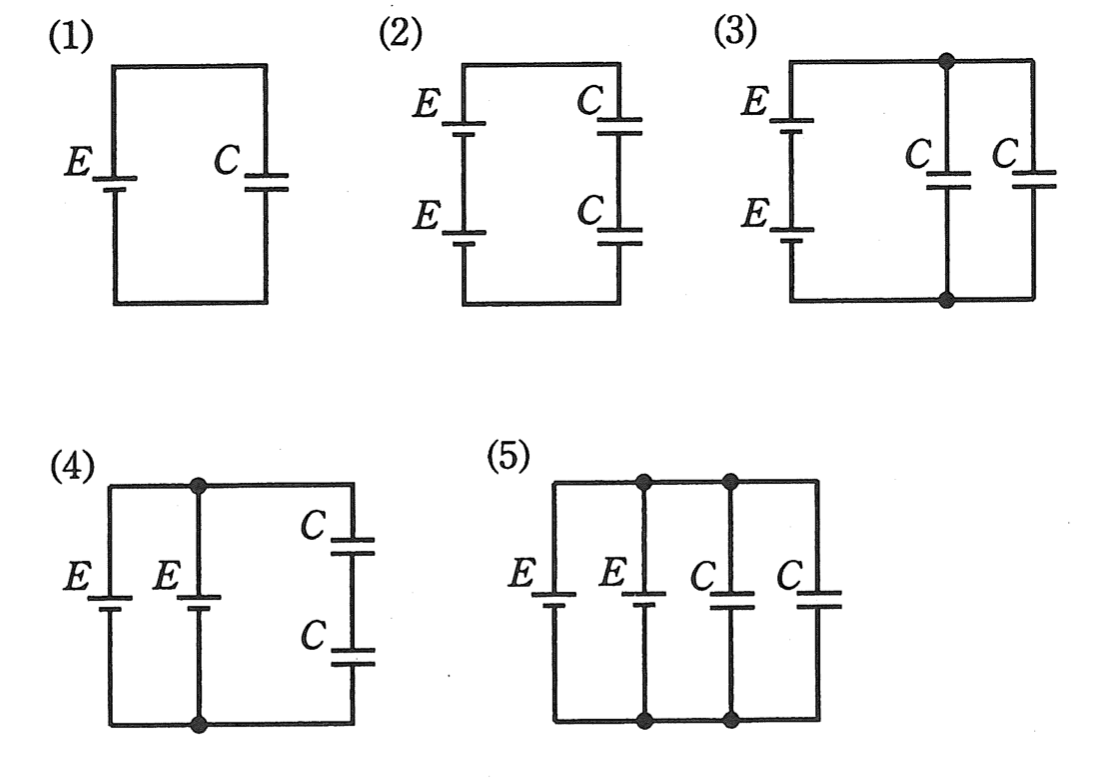
図に示す5種類の回路は,直流電圧E〔V〕の電源と静電容量C〔F〕のコンデンサの個数と組み合わせを異にしたものである。これらの回路のうちで,コンデンサ全体に蓄えられている電界のエネルギーが最も小さい回路を示す図として,正しいのは次のうちどれか。
解説
コンデンサに蓄えられるエネルギーは,コンデンサの静電容量をC,コンデンサに掛かる電圧をVとすると,\dfrac{1}{2}×C×V^2であるため,この式を用いて各回路のエネルギーを順に確認していきます。なお,回路(1)は公式通りのエネルギー量となるため,他の回路に蓄えられるエネルギーは回路(1)を基準に考えていきます。
回路(1)
公式のとおり,\dfrac{1}{2}×C×E^2となります。
回路(2)
コンデンサの合成容量が\dfrac{C}{2},コンデンサ全体に係る電圧は2Eであるため,エネルギーは\dfrac{1}{2}×\dfrac{C}{2}×4E^2=\dfrac{1}{2}×C×E^2×2となり,回路(1)の2倍のエネルギーを蓄えることができます。
回路(3)
コンデンサの合成容量が2C,電圧は2Eであるため,エネルギーは\dfrac{1}{2}×2C×4E^2=\dfrac{1}{2}×C×E^2×8となり,回路(1)の8倍のエネルギーを蓄えることができます。
回路(4)
コンデンサの合成容量が\dfrac{C}{2},電圧がEであるため,エネルギーは\dfrac{1}{2}×\dfrac{C}{2}×E^2=\dfrac{1}{2}×C×E^2×\dfrac{1}{2}となり,回路(1)の半分のエネルギー量です。
回路(5)
コンデンサの合成容量が2C,電圧がEであるため,エネルギーは\dfrac{1}{2}×2C×E^2=\dfrac{1}{2}×C×E^2×2となり,回路(1)の2倍のエネルギー量です。
以上より,回路(4)のエネルギー量が最も小さくなります。
解答
(4)