問題
最大目盛150V,内部抵抗18kΩの直流電圧計V_1と最大目盛300V,内部抵抗30kΩの直流電圧計V_2の二つの直流電圧計がある。ただし,二つの直流電圧計は直動式電気計器を使用し,固有誤差はないものとする。次の(a)及び(b)の問に答えよ。
(a)二つの直流電圧計を直列に接続して使用したとき,測定できる電圧の最大の値[V]として,最も近いものを次の(1)〜(5)のうちから一つ選べ。
(1)150 (2)225 (3)300 (4)400 (5)450
(b)次に,直流電圧450Vの電圧を測定するために,二つの直流電圧計の指示を最大目盛にして測定したい。そのためには,直流電圧計(ア)に、抵抗(イ)kΩを(ウ)に接続し,これに直流電圧計(エ)を直列に接続する。このように接続して測定することで,各直流電圧計の指示を最大目盛にして測定をすることができる。
上記の記述中の空白箇所(ア)〜(エ)に当てはまる組合せとして、正しいものを次の(1)〜(5)のうちから一つ選べ。

解説
(a)
二つの直流電圧計を直列に接続して電圧を測定するというのは,具体的には接続された二つの直流電圧計が示す値を足し算して,電圧を測定するという意味です。ある2つの抵抗が直列に接続された回路では,それぞれの抵抗に生じる電圧の合計が,その回路に加えられた電圧となります。これと同じ理屈で,二つの直流電圧計を直列に接続すると,直流電圧計の内部抵抗の大きさにより,回路全体の電圧が分圧されるため,それぞれの直流電圧計の測定値を合計することで,回路全体の電圧を測定することが可能となります。
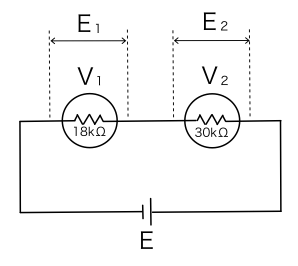
上図は問題の直流電圧計を直列にして,電圧Eを測定するときの回路図ですが,それぞれの直流電圧計の内部抵抗の大きさにより,電圧 E が E_1 と E_2 に分圧されています。
ここで注意しないといけないことは,分圧された電圧の大きさが,それぞれの直流電圧計の測定範囲を超えてはいけないということです。二つの直流電圧計それぞれの最大測定値を超えない範囲であれば,二つの直流電圧計を直列にして回路の電圧を測定することが可能です。
上記の考え方を踏まえて,問題を解いていきます。
最大目盛150Vの直流電圧計 V_1 と最大目盛450Vの直流電圧計 V_2 を電圧 E [V]の回路に接続したとき, V_1 に生じる電圧を E_1 [V], V_2 に生じる電圧を E_2 [V]とすると, E_1 , E_2 は以下のとおり表すことができます。
E_1 = E \times \dfrac{18}{18+30}
E_2 = E \times \dfrac{30}{18+30}
それぞれの直流電圧計が最大値を示すときの,回路の電圧 E の大きさを確認していきます。
まず, V_1 に最大測定値である150Vが生じるときの,回路の電圧 E [V]を求めてみます。上記の式で, E_1 = 150 として E を求めると,
E = E_1 \times \dfrac{18+30}{18} = 150 \times \dfrac{48}{18} = 400 [V]
となります。
同様に, V_2 に最大測定値である450Vが生じるときの,回路の電圧 E [V]を求めると,
E = E_2 \times \dfrac{18+30}{30} = 450 \times \dfrac{48}{30} = 480 [V]
となります。
この結果から,400 [V]以下であれば二つの直流電圧計のそれぞれの測定範囲を超えずに測定できますので,答えは(4)となります。
(b)
二つの直流電圧計を直列に接続して電圧を測定する場合,(a)の結果からその最大の測定電圧は400Vで,その理由は測定電圧が400Vを越えると V_1 の直流電圧計に生じる電圧が最大測定値を超えてしまうことでした。従ってこの問題文のとおり450Vの直流電圧を測定しようとすると, V_1 の直流電圧計には最大測定値の150Vを越える電圧が生じてしまいます。
もう一方の V_2 の直流電圧計の最大測定値は300Vであり, V_1 の直流電圧計に比べ測定範囲に余裕があります。 V_1 の直流電圧計と V_2 の直流電圧計にそれぞれ生じる電圧の大きさを調整することで, V_1 の直流電圧計に生じる電圧を小さくし, V_2 の直流電圧計に生じる電圧を大きくしてあげれば,より広い範囲の電圧を測定できそうです。
そもそも, V_1 と V_2 のそれぞれの電圧計に生じる電圧が異なるのは,それぞれの内部抵抗の大きさにより,測定しようとする電圧が分圧されることが理由でした。ですので,内部抵抗の大きさを変えることができれば,それぞれの電圧計に生じる電圧を調整することができます。だた,実際に電圧計の内部の抵抗値を変えることはできません。目的は電圧計に生じる電圧を変えることですので,内部抵抗の大きさを変える代わりに電圧計と並列に抵抗を接続すれば,接続した抵抗と電圧計の内部抵抗の合成抵抗値が小さくなり,その結果,電圧計に生じる電圧の大きさを変えることができます。これと直列に接続される電圧計に生じる電圧も,抵抗値の大きさにより分圧される比率が変わるため,単純に二つの電圧計を直列に接続したときに生じる電圧とは異なる大きさとなります。
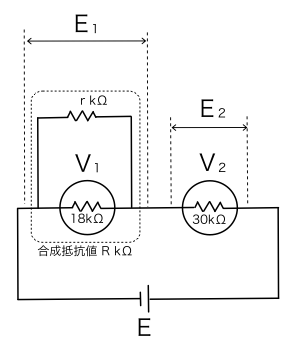
上図は問題の直流電圧計の片方に並列に抵抗を接続した場合の図です。それぞれの直流電圧計に生じる電圧は,抵抗値R[kΩ]と30[kΩ]により分圧されるため,問題(a)のときとは異なる大きさとなります。
それでは問題に戻り実際に計算していきます。450Vの電圧を測定しようとする場合, V_1 の直流電圧計には最大測定値を越える電圧が生じてしまいますので,この電圧計に並列に抵抗を接続して,この並列回路の合成抵抗値を小さくすることを考えます。
V_1 の電圧計の内部抵抗と電圧計に並列に抵抗を接続したときの合成抵抗値を R ,測定電圧を E とします。 V_2 の電圧計の内部抵抗は30kΩであることを考慮すると, V_1 の電圧計に生じる電圧 E_1 は以下の様に求まります。
E_1 = E \times \dfrac{R}{R+30}
測定電圧 E は450Vであり, V_1 の電圧計に生じる電圧 E_1 がこの電圧計の最大測定値150Vとなるときの合成抵抗 R を求めます。それぞれの値を常式に代入すると,
150 = 450 \times \dfrac{R}{R+30}
となりますので,この式から R を求めると,
\dfrac{R}{R+30} = \dfrac{1}{3}
3R = R + 30
R = 15
となります。
この結果から,合成抵抗値を15Ωとすれば, V_1 の電圧計の最大測定値を超えることなく,450Vまでの電圧を測定することが可能となります。
あとは並列に接続する抵抗値を求めるだけです。その抵抗の大きさを r とすると,抵抗の並列接続の計算方法により,
\dfrac{1}{18} + \dfrac{1}{r} = \dfrac{1}{15}
\dfrac{18 + r}{18r} = \dfrac{1}{15}
15(18+r) = 18r
3r = 270
r = 90
と求まります。
以上の結果から,「直流電圧計(ア)V_1に、抵抗(イ)90kΩを(ウ)並列に接続し,これに直流電圧計(エ)V_2を直列に接続する。」ことで,直流電圧450Vの電圧を測定することが可能となります。問題の(ア)から(エ)に当てはまる語句の組み合わせで正しいのは(2)です。
解答
(a)(4)
(b)(2)