問題
図のように,誘電体の種類,比誘電率,絶縁破壊電界,暑さがそれぞれ異なる三つの並行板コンデンサ①〜③がある。極板の形状と大きさは同一で,コンデンサの端効果,初期電荷及び漏れ電流は無視できるものとする。上側の極板に電圧V_0の直流電源を接続し、下側の極板を接地した。次の(a)及び(b)の問に答えよ。
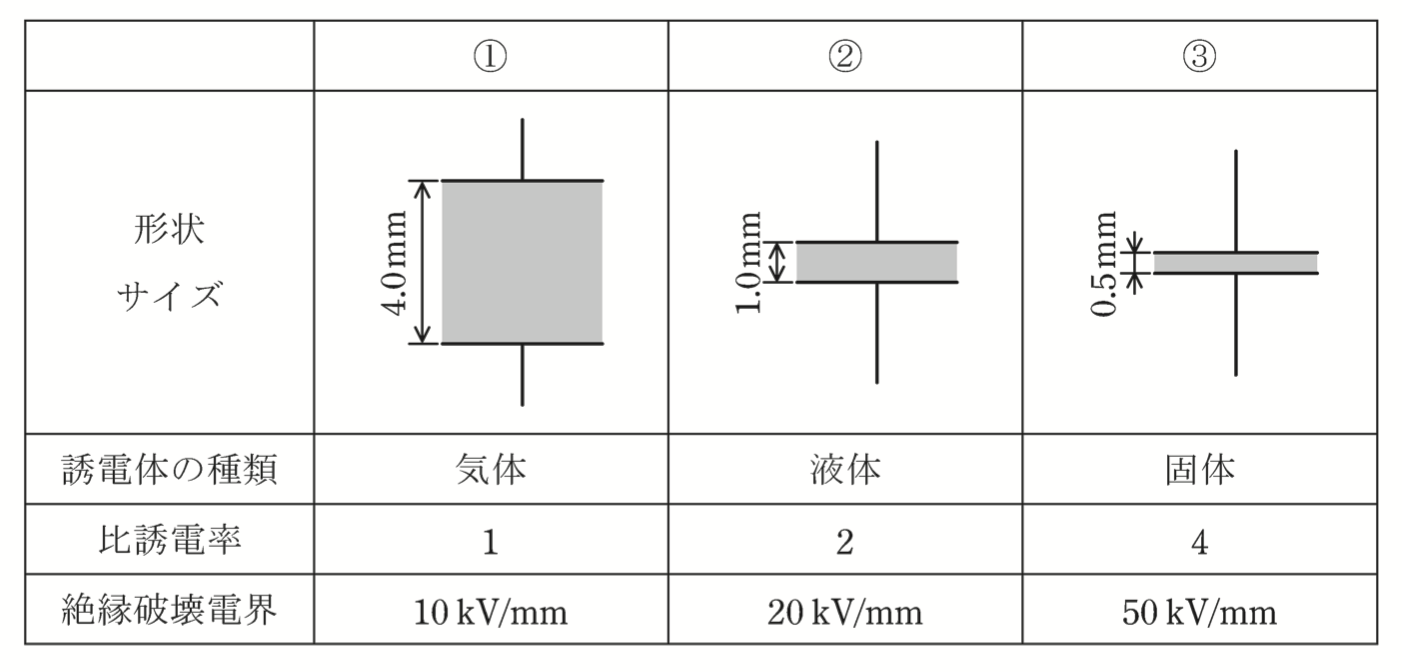
(a)各平行板コンデンサへの印加電圧の大きさが同一のとき,極板間の電界の強さの大きい順として,正しいものを次の(1)〜(5)のうちから一つ選べ。
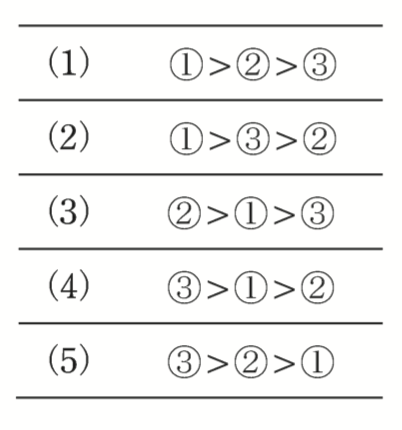
(b)各平行板コンデンサへの印加電圧をそれぞれ徐々に上昇し,極板間の電界の強さが絶縁破壊電界に達したときの印加電圧(絶縁破壊電圧)の大きさの大きい順として、正しいものを次の(1)〜(5)のうちから一つ選べ。

解説
(a)
平行板コンデンサの電極間の電界を E [V/m],電極間の距離を d [m]とすると,印可電圧 V_0 との関係は以下のとおり表すことができます。
E = \dfrac{V_0}{d}
上式より,電極間の電界の大きさは,電極間の電圧に比例し,電極間の距離とは反比例の関係にあります。
問題では電極間の電圧が一定であるため,電極間の距離が小さくなると,電極間の電界は大きくなります。従って,電極間の電界が大きい順に並べると③,②,①の順となりますので,答えは(5)です。
(b)
各平行板コンデンサが絶縁破壊電圧に達したときの印可電圧 V とし,(a)と同様に E = \dfrac{V}{d} の関係を使って,各平行板コンデンサが絶縁破壊電圧に達したときの印可電圧を順に求めていきます。
①のコンデンサは,
10 = \dfrac{V}{4}
より,
V = 40 [kV]
となります。同様に②のコンデンサは,
V = 20 \cdot 1 = 20 [kV]
となり,③のコンデンサは,
V = 50 \cdot 0.5 = 25 [kV]
となります。大きい順に並べると,①,③,②となりますので,答えは(2)です。
解答
(a)(5)
(b)(2)