問題
図1に示すエミッタ接地トランジスタ増幅回路について,次の(a)及び(b)の問に答えよ。
ただし,I_B[μA],I_C[μA]はそれぞれベースとコレクタの直流電流であり,i_b[μA],i_c[μA]はそれぞれの信号分である。また,V_{BE}[V],V_{CE}[V]はそれぞれベース−エミッタ間とコレクタ−エミッタ間の直流電圧であり,v_{be}[V],v_{ce}[V]はそれぞれの信号分である。さらに,v_{i}[V],v_{o}[V]はそれぞれ信号の入力電圧と出力電圧,V_{CC}[V]はバイアス電源の直流電圧,R_1[kΩ]とR_2[kΩ]は抵抗,C_1[F],C_2[F]はコンデンサである。なお,R_2 = 1kΩであり,使用する信号周波数においてC_1,C_2のインピーダンスは無視できるほど十分小さいものとする。
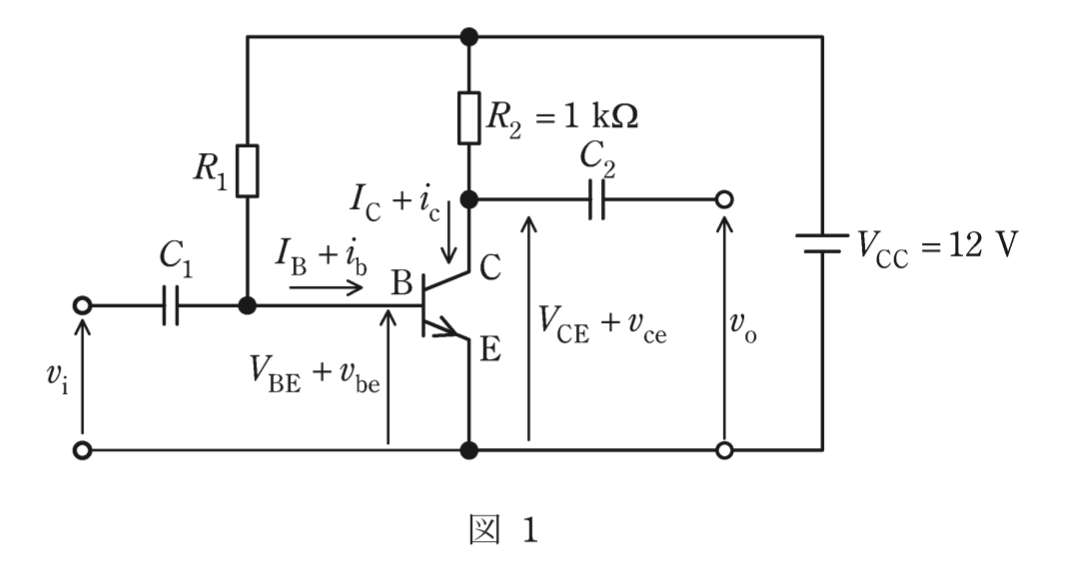
(a)図2はトランジスタの出力特性である。トランジスタの動作点をV_{CE} = \dfrac{1}{2} V_{CC} = 6Vに選ぶとき,動作点でのベース電流I_Bの値[μA]として,最も近いものを次の(1)〜(5)のうちから一つ選べ。
(1)20 (2)25 (3)30 (4)35 (5)40
(b)小問(a)の動作点において,図1の回路に交流信号電圧v_iを入力すると,最大値10μAの交流信号i_bと小問(a)の直流電流I_Bの和がベース(B)に流れた。このとき,図2の出力特性を使って求められる出力交流信号電圧v_o(= v_{ce} )の最大値[V]として,最も近いものを次の(1)〜(5)のうちから一つ選べ。
ただし,動作点付近においてトランジスタの出力特性は直線で近似でき,信号波形はひずまないものとする。
(1)1.0 (2)1.5 (3)2.0 (4)2.5 (5)3.0
解説
(a)
図2のトランジスタの出力特性には,I_Bの値ごとの特性が複数描かれていますが,縦軸のI_Cの値と横軸のV_{CE}の値が分かれば,I_Bの値を特性図から求めることができます。(当然ながら,I_CとV_{CE}の値によっては,グラフ上の交点にI_Bの特性が描かれていない場合も考えられますが,試験問題なのでそれは考えなくても大丈夫です。)問題文よりV_{CE}の値は6Vと分かっているので,後はI_Cの値を求めれば答えを得ることができます。
I_C の値は R_2 に生じる電圧から求めることができます。 R_2 に生じる電圧を V_{R2} とすると,
V_{R2} = V_{CC} - V_{CE}
であり,動作点では信号分の電圧 v_{ce} は0Vですので,この式に V_{CE} = 6[V]を代入して,
I_C を求めると,
I_C = \dfrac{V_{R2}}{R_2} = \dfrac{V_{CC} - V_{CE}}{R_2} = \dfrac{12-6}{1 \times 10^{3}} = 6 \times 10^{-3} = 6 [mA]
特性図より, I_C が6mA, V_{CE} = 6[V]のときのグラフの交点を確認すると,ちょうど交点のところに30μAの特性図が描かれていますので I_B = 30 [mA]であることが分かります。
したがって答えは(3)となります。
(b)
問題(a)で動作点での I_B の値は30mAでしたので,最大10μAの交流信号が加わると I_B の値は40mAとなります。問題(a)と同様に,信号成分 v_{ce} が加算されたときのコレクタ-エミッタ間の電圧 V_{CE} の値を, I_C の値を求めてから, I_B = 40 [mA]の特性の線上で交点となる, V_{CE} の値を見つけるという方法で求めたいですが, I_C の値は,
I_C = \dfrac{V_{CC} - V_{CE}}{R_2}
の式からは,直接求めることができません。それは,この式の中に V_{CE} が含まれており, V_{CE} はこれから求めようとしているとおり,交流信号i_bが直流電流I_Bに加算されると,値が変化するためです。
ここでこの式をよく見てみると,この式に含まれる V_{CC} と R_2 は変化しない値ですので,これらの値をこの式に代入すると, I_C と V_{CE} との関係を表す式を得ることが出来ます。その関係は,
I_C = \dfrac{V_{CC} - V_{CE}}{R_2} = \dfrac{12 - V_{CE}}{1 \times 10^3} [A] = (12 - V_{CE}) \times 10^{-3} [A]
= 12 - V_{CE} [mA]
となりますが,問題の図2は縦軸が I_C ,横軸が V_{CE} ですので,この関係式を図2に描くことで, I_B = 40 [mA]の特性の線と交わる点を見つけることが可能になります。
V_{CE} = 0 のとき, I_C は,
I_C = 12 - V_{CE} = 12 [mA]
であり, I_C = 0 のとき, V_{CE} は,
0 = 12 - V_{CE}
V_{CE} = 12
と求まります。
I_C と V_{CE} との関係は一次式であり直線で表されるため, V_{CE} = 0, I_C = 12 の点と I_C = 0, V_{CE} = 12 の点を結ぶ直線を図2に描くと,以下のとおりとなります。
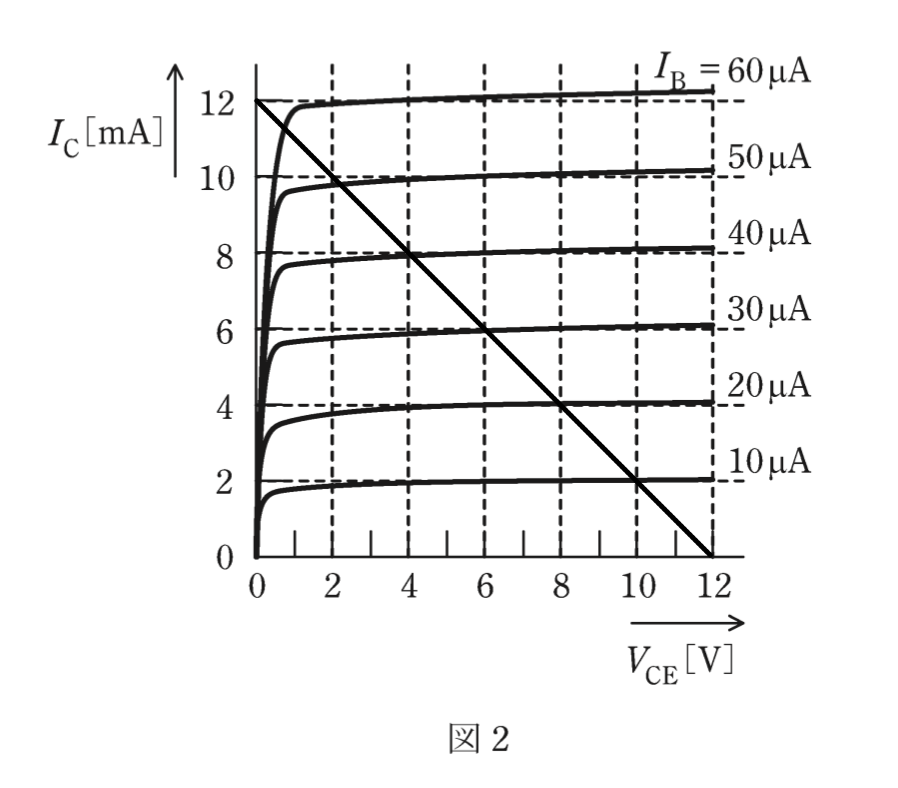
描いた直線と I_B = 40 [mA]の特性の線との交点を求めると, I_C = 8, V_{CE} = 4 となります。
問題で求められているのは,「出力交流信号電圧v_o(= v_{ce} )の最大値[V]」です。先ほどグラフから求めた V_{CE} の値は,信号成分 v_{ce} が加算されたときのコレクタ-エミッタ間の電圧ですので,出力される交流信号電圧の最大値は,動作点の電圧6Vからの変位量となるため,
6-4=2 [V]
となります。
したがって答えは(3)となります。
解答
(a)(3)
(b)(3)