電験一種 令和4年度 理論　問1『電位と電界を解析的に求める方法に関する問題』

問題

次の文章は，複素数を用いて2次元の電界を解析的に求める手法に関する記述である。文中の$\fbox{　　}$に当てはまる最も適切なものを解答群の中から選べ。
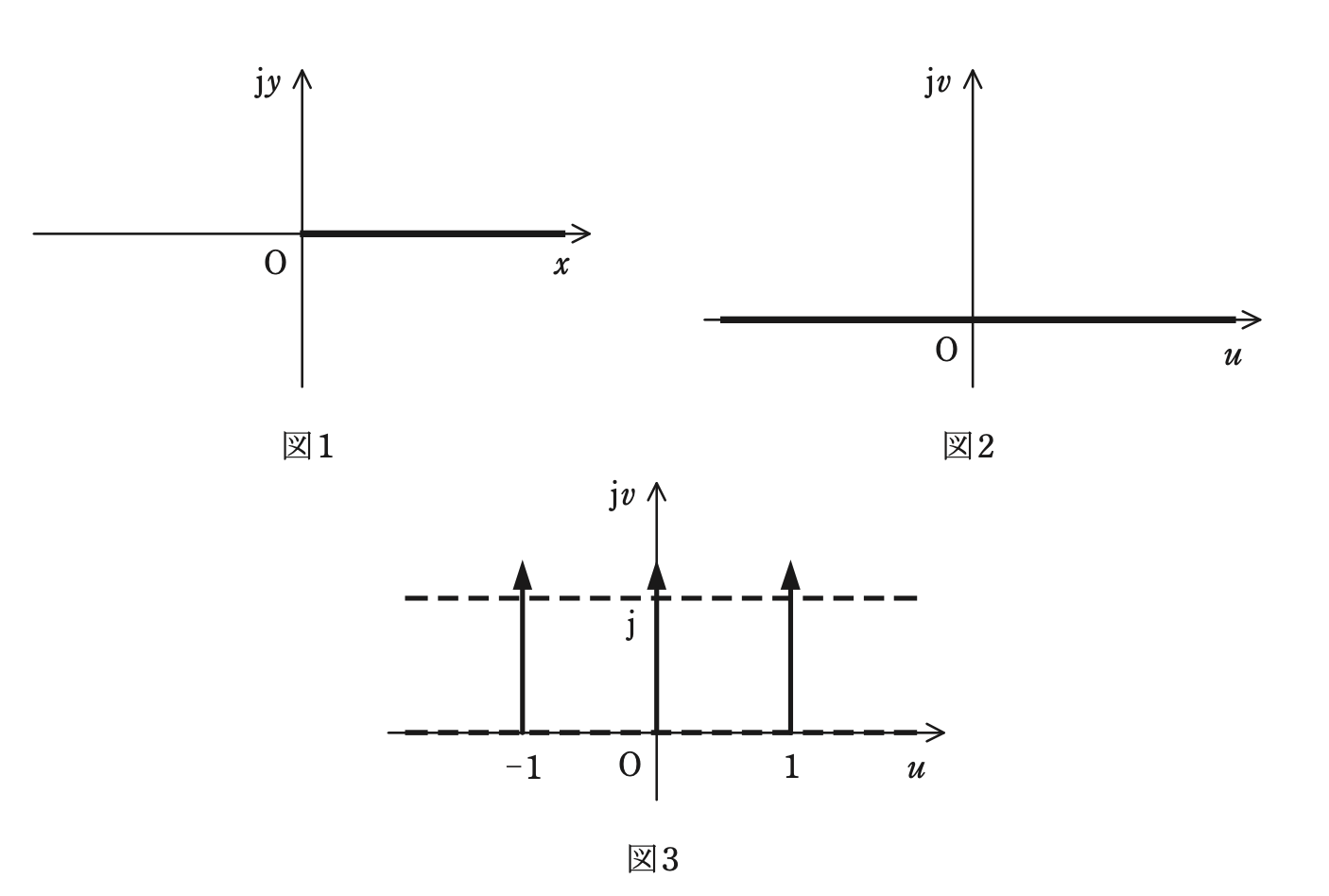
図1のように，$z = x + jy$で表される複素平面上で，$y = 0$，$x ≧ 0$で記述される原点が端で無限に長く細い電極に電圧が印加されているとき，等角写像法を用いて平面上の電界及び電位を解析的に求めることができる。
等角写像法では，電気力線と等電位線が既知である別の複素平面 $w = u +jv$を考え，$z$に写像する写像関数$z = f (w)$を与える。$f (w)$が連続で微分可能であれば，電気力線と等電位線が$\fbox{（1）}$という関係が，写像を行っても保たれる。
ここで，図2のように，複素平面$w$の $v ≧ 0$の範囲において，$u$ 軸上に置かれた無限に長い電極は，$f(w) = w^2$により，$x + jy = (u + jv)^2$の関係が成り立つことより，$z$上において図1に示す電極に写像される。$w$には，$u$ 軸と平行に等電位線が，$v$軸と平行に電気力線が構成されるので，それらを$z$上に写像すれば $z$上での等電位線と電気力線が解析的に求められることになる。
例えば，図3において$v = 1$の式で表される等電位線は，$z$上では$\fbox{（2）}$の式で表される。また，$u = 0$及び$u = 1$の式で表される2本の電気力線は，$z$上では それぞれ$\fbox{（3）}$及び$\fbox{（4）}$の式で表される。ただし，各図において，実線の矢印は電気力線，破線は等電位線を表す。
これらのことにより，図3に描かれた電気力線と等電位線を$z$上に写像すると$\fbox{（5）}$の図が得られる。

解説

通常の教科書には載っていないような方法で電界を求める問題ですが，電験1種ではこのような問題が出題されることがあります。このような問題の場合，その方法そのものを知らなくても，電界や電位に関しての基本的なことが分かっていれば，順を追って解けるようになっていることが多いです。

（1）

問題は等角写像法の説明の中の一文ですが，聞かれていることは「電気力線」と「等電位線」との関係がどうなっているかということです。

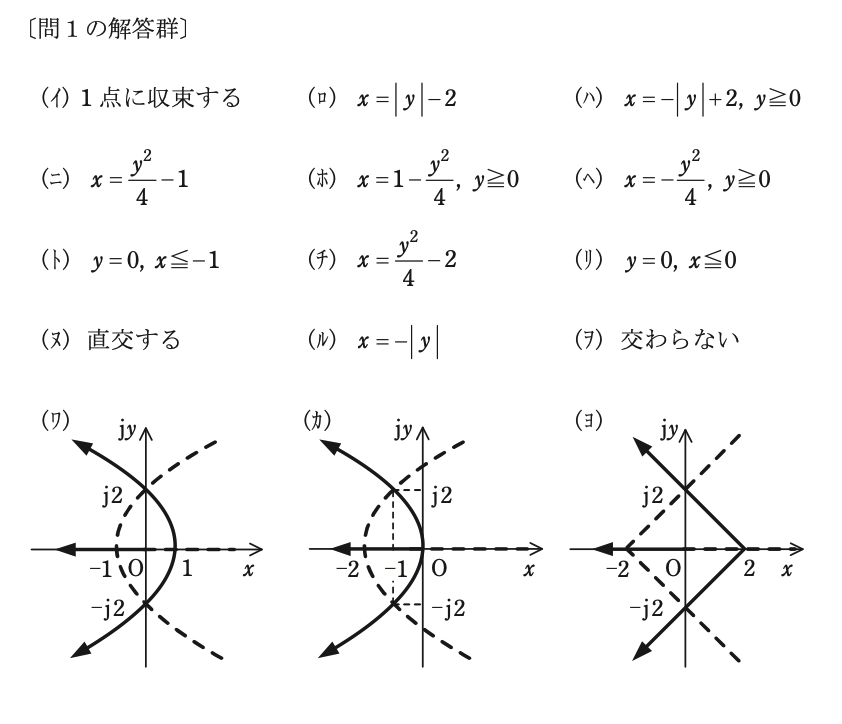
解答の選択肢で候補となるのは，「（ｲ）1点に収束する」，「（ﾇ）直交する」，「（ｦ）交わらない」のどれかですが，電気力線と等電位線は常に直交していますので，正解は「（ﾇ）直交する」になります。

（2）

図3は複素平面 $w$を示しており，複素平面 $z$との関係は，問題文に記載されているとおり，$z = f(w) = w^2$という関数で表されています。

図3で $v = 1$の式で表される等電位線は，下図の赤枠で囲った部分です。

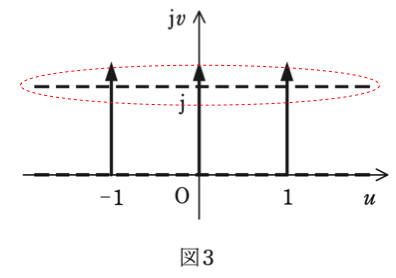
$v = 1$は複素平面の虚軸の値だけを示していますので，これを虚軸も含めた形の式で表すと，

$w = u + j$

となります。これを写像関数$z = f(w) = w^2$を使って複素平面$z$へ変換すると，

$z = (u + j)^2 = u^2 + j2u + j^2 = u^2 -1 + j2u$

となります。

複素平面$z$では，実軸が$x$，虚軸が$y$ですので，上式より

$x = u^2 -1$
$y = 2u$

となりますので，これらの式から$u$を消去すると，$x$と$y$の関係が得られます。

$y$と$u$の関係式から

$u = \dfrac{y}{2}$

と求まりますので，この$u$を$x$の式に代入すると，

$x = \left(\dfrac{y}{2}\right)^2 -1 = \dfrac{y^2}{4} - 1$

となります。

したがって，正解は「（ﾆ）$x = \dfrac{y^2}{4} - 1$」です。

この結果を複素平面$z$上で表すと以下のようになります。

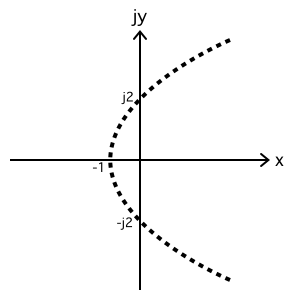
図3の複素平面 $w$上では一直線であった等電位線が，複素平面$z$上では放物線で表されています。

図2で示される一直線に無限に長い電極が作る電位は，図3で示されているように電極に並行になることは電験3種の問題でもあるように，比較的簡単な計算で求めることができます。しかしながら，図1で示されるような原点から片側に一直線に長い電極の場合は，上図で示されるような電位を電磁気学に基づく計算で求めることになるため，少し手間がかかります。

等角写像法を使った方法では，電磁気学による計算で電位と電界を求めるのではなく，あらかじめ結果が分かっている電位と電界を，写像関数を使って間接的に求めています。

一直線に無限に長い電極を，原点から片側に長い電極に変換するための写像関数が分かれば，一直線に無限に長い電極によって生じる電界と電位をその写像関数を使って変換し，片側に長い電極が作る電界と電位を求めるという方法です。

写像関数に「写像」という言葉が含まれているように，あたかも写像関数を使って写し出される世界を見て結果を求めるようなイメージでしょうか。

（3）

$u = 0$についても（2）と同様の方法で求めます。

図3で $u = 0$の式で表される電気力線は，下図の赤枠で囲った部分です。

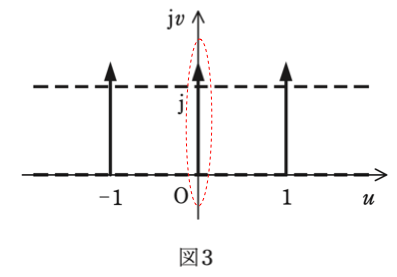
今回は電気力線ですので，複素平面の虚軸と並行な線になっています。$u = 0$は実軸の値だけを示していますので，これを虚軸も含めた形の式で表すと，

$w = jv$

となります。これを写像関数$z = f(w) = w^2$を使って複素平面$z$へ変換すると，

$z = (jv)^2 = -v^2$

となります。

この結果，複素平面$z$では，実部の値しかありませんので，

$x = -v^2$
$y = 0$

となります。

複素平面$z$では$x$の値は常に負の値となり，$y$は常に0ですので，正解は「（ﾘ）$y = 0，x \leqq 0$」となります。

この結果を複素平面$z$上で表すと以下のようになります。

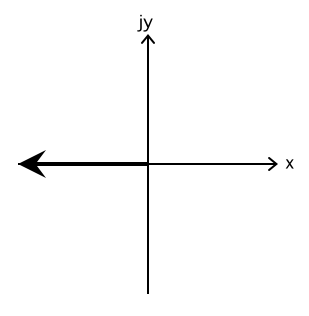
今回は電気力線ですので，$z$上でも矢印が付いています。

（4）

$u = 1$についても同様に求めます。

図3で $u = 1$の式で表される電気力線は，下図の赤枠で囲った部分です。

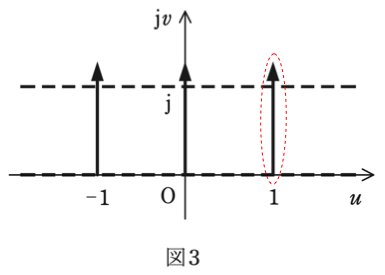
$u = 1$は実軸の値だけを示していますので，これを虚軸も含めた形の式で表すと，

$w = 1 + jv$

となりますので，これを写像関数を使って複素平面$z$へ変換すると，

$z = (1+jv)^2 = 1 + j2v -v^2 = 1 - v^2 + j2v$

となるため，複素平面$z$では，

$x = 1 - v^2$
$y = 2v$

となります。$y = 2v$より

$v = \dfrac{y}{2}$

であるため，これを$x$の式に代入すると，

$x = 1 - \dfrac{y^2}{4}$

となります。したがって正解は「（ﾎ）$x = 1 - \dfrac{y^2}{4} ，y \geqq 0$」となります。

$y \geqq 0$が記載されているのは，図3では$v$が正の値しかとらない図になっているためと思われます。実際の電気力線は導体を中心にして$v$の負の側にも矢印が伸びるような図になるかと思います。

電気力線が$v$の負の側にも伸びることを考慮して，この結果を複素平面$z$上で表すと以下のようになります。

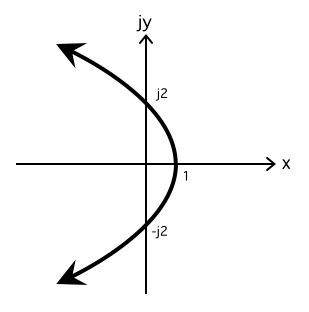
（5）

（2），（3），（4）で得られた複素平面$z$上のグラフを合成すると，（ﾜ）に記載されたグラフになりますので，正解は（ﾜ）です。

解答

（1）ヌ　（2）ニ　（3）リ　（4）ホ　（5）ワ