問題
次の文章は,電荷を帯びた球の作る電界に関する記述である。文中の\fbox{ }に当てはまる最も適切なものを解答群の中から選べ。
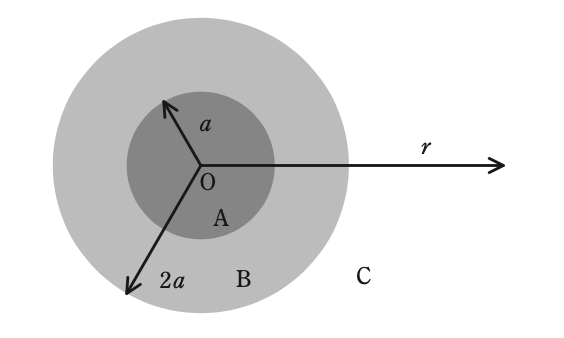
図のように,真空中の原点Oからの距離がrであるとき,0≦r≦a, a<r≦2a, r>2a の領域をそれぞれ領域A,B,Cとする。領域AとBにはそれぞれ電荷密度 + \rho , -\dfrac{\rho}{7} で電荷が一様に分布している。また,領域 C に電荷は存在しない。ただし,\rho > 0であり,全ての領域の誘電率は真空中の誘電率 \epsilon_0である。
このとき,領域Aに存在する電荷の合計は\fbox{ (1) }である。
また,球の中心から距離rの位置におけるr方向の電界E(r) は,
領域A (0 ≦ r ≦ a ) のとき\fbox{ (2) }
領域B( a < r ≦ 2a )のとき\fbox{ (3) }
領域C( r > 2a )のとき\fbox{ (4) }
である。
このとき,E(r) の符号に着目すると,r \rightarrow \infty の無限遠点を電位の基準とした場合に,中心 O (r = 0 ) の電位の符号は,\fbox{ (5) }。

解説
(1)
領域Aにおける電荷の合計は,領域Aの体積に電荷密度をかけることで求めることができます。
領域Aの体積は半径がaであるので,
\dfrac{4}{3}\pi a^3
です。これに領域Aの電荷密度 \rho をかけて,電荷の合計を求めると,
\dfrac{4}{3}\pi a^3 \rho
となりますので,答えは(ヲ)です。
(2)
ガウスの法則を使って電界を求めます。
ガウスの法則では,原点からの距離rを半径とする球の表面上の電界がE(r),内部の電荷をQ,誘電率が \epsilon_0のとき,
\int_S E(r) dS = \dfrac{Q}{\epsilon_0}
と表されます。
左辺の積分は,半径rの球の表面積に電界E(r)をかけたものですので,
4 \pi r^2 E(r)
となり,ガウスの法則の式は,
4 \pi r^2 E(r) = \dfrac{Q}{\epsilon_0}
となります。この式から電界E(r)を求めると,
E(r) = \dfrac{Q}{4 \pi r^2 \epsilon_0}
となります。
(2)で求めるのは,半径rが領域Aにあるときの,rの位置におけるr方向の電界E(r) です。ガウスの法則を使ってこの電界を求めるためには,半径rの球の内部の電荷量を求める必要がありますので,まずはこの電荷量を求めます。
領域Aの電荷の密度が \rho ,半径rの球の体積は \dfrac{4}{3} \pi r^3 ですので,この領域の電荷の大きさを Q_{Ar} とすると,
Q_{Ar} = \dfrac{4}{3} \pi r^3 \rho
と求まります。
これを先ほどのガウスの法則から求めた電界E(r)の式に代入すると,
E(r) = \dfrac{Q_{Ar}}{4 \pi r^2 \epsilon_0} = \dfrac{1}{4 \pi r^2 \epsilon_0} \dfrac{4}{3} \pi r^3 \rho = \dfrac{r \rho}{3 \epsilon_0}
となりますので,答えは(ニ)です。
(3)
領域Bについても同様にガウスの法則を使います。
原点からの距離rが領域Bにあるとき,その半径の内部にある電荷の大きさを考えます。ここで注意をしないといけないのは,半径rが領域Bにあるとき,その半径の内側には領域Bとは電荷密度の異なる領域Aがあるため,その半径の内部にある電荷は領域Aと領域Bの両方を考慮しないといけないということです。
まずは領域Aの電荷量を求めます。半径rが領域Aにあるときの電荷量は問題(2)で求めたとおり,
Q_{Ar} = \dfrac{4}{3} \pi r^3 \rho
ですので,領域A全体の電荷量Q_Aは,半径rに領域Aの球の半径の大きさaを代入して,
Q_A = \dfrac{4}{3} \pi a^3 \rho
と求まります。
次に領域Bの電荷量を求めます。
領域Bの電荷密度が問題で与えられていますので,領域Bの体積の大きさを求めて,その大きさに電荷密度をかけることで,領域Bの電荷量を求めることができます。
半径rが領域Bにあるときの,領域Bのみの球の体積の大きさは,内部にある領域Aの体積の大きさを引くことで求められます。
半径rの球の体積は
\dfrac{4}{3}\pi r^3
ですので,これから領域Aの体積の大きさ
\dfrac{4}{3}\pi a^3
を引くと
\dfrac{4}{3}\pi r^3 - \dfrac{4}{3}\pi a^3 = \dfrac{4}{3}\pi (r^3 - a^3)
となります。これに領域Bの電荷密度 -\dfrac{\rho}{7} をかけると,半径rが領域Bにあるときの領域Bの電荷量Q_{Br}は,
Q_{Br} = \dfrac{4}{3}\pi (r^3 - a^3) (-\dfrac{\rho}{7} ) = -\dfrac{4}{21}\pi \rho (r^3 - a^3)
と求まります。
したがって,半径rが領域Bにあるときの,領域Aも考慮したその内部の電荷量Q_{ABr}は,先ほど求めたQ_Aとの和ですので,
Q_{ABr} = Q_{Br} + Q_A = -\dfrac{4}{21}\pi \rho (r^3 - a^3) + \dfrac{4}{3} \pi a^3 \rho
= -\dfrac{4}{21}\pi \rho (r^3 - a^3) + \dfrac{28}{21} \pi a^3 \rho
= -\dfrac{4}{21}\pi \rho r^3 + \dfrac{4}{21} \pi a^3 \rho + \dfrac{28}{21} \pi a^3 \rho
= \dfrac{32}{21} \pi a^3 \rho - \dfrac{4}{21}\pi \rho r^3
となります。
最後にガウスの法則を使ってこの位置における電界 E(r) を求めると,
E(r) = \dfrac{Q_{ABr}}{4 \pi r^2 \epsilon_0} = \dfrac{1}{4 \pi r^2 \epsilon_0} ( \dfrac{32}{21} \pi a^3 \rho - \dfrac{4}{21}\pi \rho r^3 )
= \dfrac{\pi \rho}{\pi r^2 \epsilon_0} ( \dfrac{8}{21} a^3 - \dfrac{1}{21} r^3 )
= \dfrac{\rho}{21 \epsilon_0} ( \dfrac{8 a^3}{r^2} - r )
となり,答えは(ホ)です。
(4)
半径rが領域Cにあるとき,半径rの球の内部にある電荷量は,領域Aと領域Bの合計の電荷量となります。
領域Aと領域Bの全体の電荷量Q_{AB}は,(3)で求めたQ_{ABr}のrに,領域Bの半径の大きさ2aを代入することで求まります。
Q_{ABr} = \dfrac{32}{21} \pi a^3 \rho - \dfrac{4}{21}\pi \rho r^3
ですので,これに r = 2a を代入すると,
Q_{ABr} = \dfrac{32}{21} \pi a^3 \rho - \dfrac{4}{21}\pi \rho (2a)^3
= \dfrac{32}{21} \pi a^3 \rho - \dfrac{4}{21}\pi \rho 8a^3
= \dfrac{32}{21} \pi a^3 \rho - \dfrac{32}{21}\pi \rho a^3 = 0
となり,内部の電荷量の合計は0となります。
したがって,半径rが領域Cにあるときの,rの位置における電界 E(r) は0になり,答えは(ワ)です。
(5)
電界と電位との関係をイメージするために,問題とは関係なく,点電荷について考えます。
無限に離れた点を電位の基準とした場合,電荷が正であれば電位は電荷に近づくほど正の値で大きくなり,電荷が負であれば電位は電荷に近づくほど負の値で大きくなります。また,正の電荷が作る電界は電荷の位置から遠方に向かって放射状に広がり,電界の強さは正となります。負の電荷が作る電界は,遠方から電荷に向かう方向に放射状に集まり,電界の強さは負となります。
このイメージをもって,問題を考えます。
問題(2)から(4)で電界の強さを求めました。中心からの距離rの位置における電界の強さを改めて記載すると以下のようになります。
0 ≦ r ≦ a のとき,電界は E(r) = \dfrac{Q}{4 \pi r^2 \epsilon_0}で正の値
a < r ≦ 2a のとき,電界は E(r) = \dfrac{r \rho}{3 \epsilon_0} で正の値
r > 2a のとき,電界は0
問題にあるように,電界の符号(強さ)に着目すると,上記のとおり0から正の値となっています。正の点電荷の場合,電荷の周囲の電界が正であり,電位も正でしたので,電荷の中心の位置であるOの電位の符号は,同様に正となりますので,答えは(ル)です。
解答
(1)ヲ (2)ニ (3)ホ (4)ワ (5)ル