問題
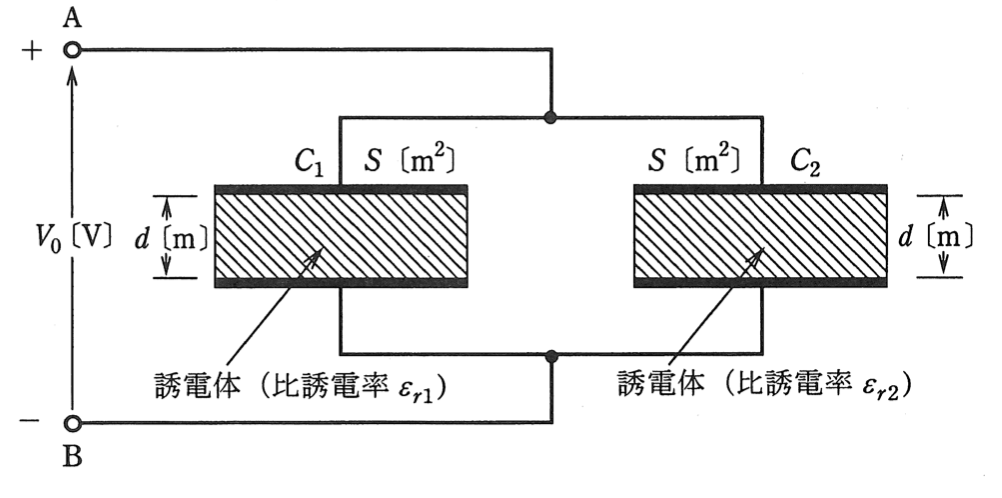
電極板面積と電極板間隔が共にS〔m2〕とd〔m〕で,一方は比誘電率がε_{r1}の誘電体からなる平行平板コンデンサC_1と,他方は比誘電率がε_{r2}の誘電体からなる平行平板コンデンサC_2がある。いま,これらを図のように並列に接続し,端子A,B間に直流電圧V_0〔V〕を加えた。このとき,コンデンサC_1の電極板間の電界の強さをE_1〔V/m〕,電束密度をD_1〔C/m2〕,また,コンデンサC_2の電極板間の電界の強さをE_2〔V/m〕,電束密度をD_2〔C/m2〕とする。両コンデンサの電界の強さE_1〔V/m〕とE_2〔V/m〕はそれぞれ(ア)であり,電束密度D_1〔C/m2〕とD_2〔C/m2〕はそれぞれ(イ)である。したがって,コンデンサC_1に蓄えられる電荷をQ_1〔C〕,コンデンサC_2に蓄えられる電荷をQ_2〔C〕とすると,それらはそれぞれ(ウ)となる。
ただし,電極板の厚さ及びコンデンサの端効果は,無視できるものとする。また,真空の誘電率をε_0〔F/m 〕とする。
上記記述中の空欄(ア),(イ)及び(ウ)に当てはまる式として,正しいものを組み合わせたのは次のうちどれか。

解説
(ア)はコンデンサの内部の電界の強さを求める問題です。
コンデンサの内部の電界の強さは、コンデンサの両端の電位差(電圧)とコンデンサの板間の距離が分かっていれば、単位が表すように、電位差/距離で求まります。今回の問題ではコンデンサは並列接続で,コンデンサの板間の距離は共に同じであるため,
E_1=\dfrac{V_0}{d},E_2=\dfrac{V_0}{d}
と電界の強さは同じになります。
(イ)はコンデンサ内部の電束密度を求める問題です。
電界はコンデンサの内部の物質には関係なく、電位差と距離のみで決まりますが、電束密度はコンデンサ内部の物質も考慮したらどうなるかを表すものであり,電束密度=電界×誘電率で表されます。誘電率は真空の誘電率に比誘電率を掛けたものであるので,
D_1=ε_0ε_{r1}E_1,D_2=ε_0ε_{r2}E_2
となります。(ア)で求めたE_1,E_2を上記の式に代入すると,
D_1=\dfrac{ε_0ε_{r1}V_0}{d},D_2=\dfrac{ε_0ε_{r2}V_0}{d}
となります。
(ウ)はコンデンサに蓄えられる電荷量を求める問題です。
コンデンサに蓄えられる電荷量は,コンデンサの容量とコンデンサに加えられる電圧(電位差)との積で求められます。式で表すと,
Q_1=C_1×V_0,Q_2=C_2×V_0
となります。ここで,C_1とC_2を電極板面積と電極板間隔で表現する必要があります。
コンデンサの容量はコンデンサの電極板面積に比例,電極板間の距離に反比例し、内部の誘電率の大きさに比例します。
今回の問題では両方のコンデンサともに面積,距離が同じで,内部の誘電体の誘電率のみが異なるため,
C_1=ε_0ε_{r1}\dfrac{S}{d},C_2=ε_0ε_{r2}\dfrac{S}{d}
となり、これをQ_1,Q_2の式に代入すると、
Q_1=\dfrac{ε_0ε_{r1}}{d}SV_0,Q_2=\dfrac{ε_0ε_{r2}}{d}SV_0
となります。
以上より、解答は(4)となります。
解答
(4)