電験三種 令和2年度 機械　問14『論理回路の論理式に関する問題』

問題

入力信号A，B及びC，出力信号Xの論理回路の真理値表が次のように示されたとき，Xの論理式として，正しいものを次の（1）〜（5）のうちから一つ選べ。

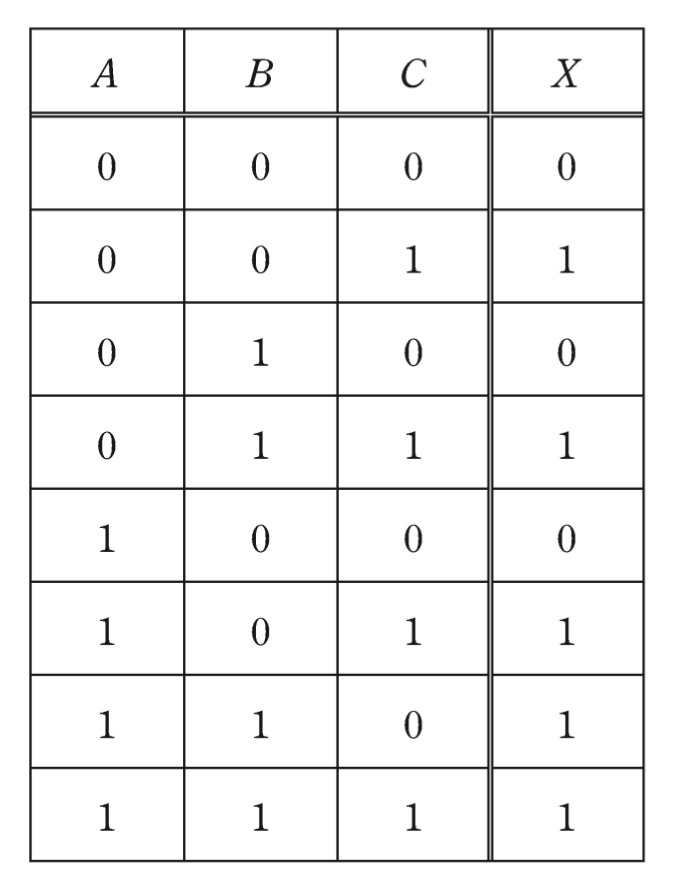
（1）　 A \cdot B + A \cdot \overline{C} + B \cdot C
（2）　 A \cdot \overline{B} + A \cdot \overline{C} + \overline{B} \cdot \overline{C}
（3）　 A \cdot \overline{B} + C + \overline{A} \cdot B
（4）　 B \cdot \overline{C} + \overline{A} \cdot B + \overline{B} \cdot C
（5）　 A \cdot B + C

解説

真理値表から論理式を導き出す方法は，真理値表の入力と出力の関係を見ながら論理式を考えることもできますが，公式に則って導く方法もあります。最初に公式に則って導く方法を説明し，最後に論理式を力技で考える方法の例を紹介します。

方法1　主加法標準形を用いる方法
真理値表で出力が1であるものを選び出し，それぞれの入力の論理積が1になるように表現し，最後にその論理積どうしの論理和を求めると，真理値表の論理式が得られるという方法です。

言葉で書いても分かりにくいと思いますので，実際に問題に適用してみます。

まず，問題の真理値表から出力が1であるものを選びます。表の上から順番に選ぶと以下のとおりとなります。

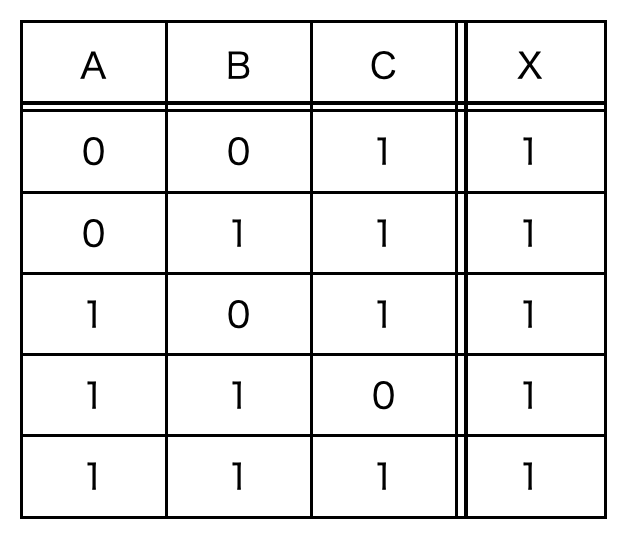
出力が1となるものは全部で5つありますが，それぞれの入力の論理積が1になるように順番に表現していきます。

表の一番上にある入力は，AとBが0，Cが1ですので，これらの入力の論理積が1となるためには，

\overline{A} \cdot \overline{B} \cdot C

である必要があります。

その次の入力はAが0，BとCが1であるため，これらの入力の論理積が1となるように表現すると，

\overline{A} \cdot B \cdot C

となります。以下，同様に出力が1になるように入力の論理積で表現すると，

A \cdot \overline{B} \cdot C
A \cdot B \cdot \overline{C}
A \cdot B \cdot C

最後に，得られたそれぞれの入力の論理積の論理和を求めると，以下のようになります。

\overline{A} \cdot \overline{B} \cdot C + \overline{A} \cdot B \cdot C + A \cdot \overline{B} \cdot C + A \cdot B \cdot \overline{C} + A \cdot B \cdot C

この論理式を簡略化すると，

\overline{A} \cdot \overline{B} \cdot C + \overline{A} \cdot B \cdot C + A \cdot \overline{B} \cdot C + A \cdot B \cdot \overline{C} + A \cdot B \cdot C
= \overline{A} \cdot C \cdot (\overline{B} + B) + A \cdot C \cdot (\overline{B} + B) + A \cdot B \cdot \overline{C}
= \overline{A} \cdot C + A \cdot C + A \cdot B \cdot \overline{C}
= C \cdot (\overline{A} + A) + A \cdot B \cdot \overline{C}
= A \cdot B \cdot \overline{C} + C
= A \cdot B + C

と求まり，答えは（5）となります。

※ 論理式を簡略化するにあたっては，このページの下の方に記載した補足の公式を使っています。

方法2　主乗法標準形を用いる方法
真理値表で出力が0であるものを選び出し，それぞれの入力が全て0になるような論理和で表現し，最後にその論理和どうしの論理積を求めると，真理値表の論理式が得られるという方法です。

こちらも言葉で書いても分かりにくいと思いますので，実際に問題に適用してみます。

まず，問題の真理値表から出力が0であるものを選びます。表の上から順番に選ぶと以下のとおりとなります。

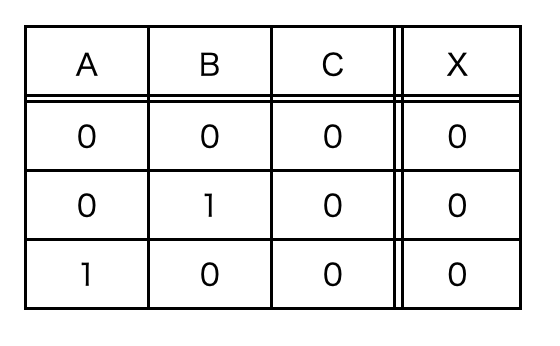
出力が0となるものは全部で3つありますが，それぞれの入力が全て0になるような論理和を順に表現します。

表の一番上にある入力は，A，B，Cがすべて0ですので，これらの論理和はそのまま，

A + B + C

となります。

その次の入力はAとCが0，Bが1であるため，これらの入力が全て0のときの論理和で表現すると，

A + \overline{B} + C

となります。

最後の入力は，Aが1，BとCが0であるため，同様に表現すると，

\overline{A} +B + C

となります。

得られたそれぞれの入力の論理和の論理積を求めると，以下のようになります。

( A + B + C ) \cdot ( A + \overline{B} + C ) \cdot ( \overline{A} +B + C )

この論理式を簡略化します。まず，前の2つの論理和の論理積を展開しますが，その際，補足に記載している関係式を使うと，

( A + B + C ) \cdot ( A + \overline{B} + C )
= A \cdot A + A \cdot \overline{B} + A \cdot C
　　+ B \cdot A + B \cdot \overline{B} + B \cdot C
　　　　+ C \cdot A + C \cdot \overline{B} + C \cdot C
= A + A \cdot \overline{B} + A \cdot C + A \cdot B + B \cdot C + \overline{B} \cdot C + C
= A + A \cdot ( \overline{B} + B) + A \cdot C + C ( B + \overline{B} ) + C
= A + A \cdot C + C = A + C

となります。これと最後の論理和( \overline{A} +B + C )との論理積を展開すると，

( A + C ) \cdot (\overline{A} + B + C )
= A \cdot \overline{A} + A \cdot B + A \cdot C + \overline{A} \cdot C + B \cdot C + C
= A \cdot B + C \cdot ( A + \overline{A} ) + C = A \cdot B + C

となり，答えは方法1と同じく（5）になります。

方法3　力技で解く方法

簡単な真理表であれば，真理値表を見て論理式を考えることもできます。

問題の真理値表で出力と入力を比較したとき，入力のCだけは出力と常に同じ値となっています。このため，入力Cと何かとの論理和として

○○+ C

というような論理式になっていることが予想されます。

○○の箇所は，AとBの入力がどのように表現されるかということですので，AとBと出力との関係を確認していきます。

真理値表で出力が1であるところは，Cが1であれば，A，Bがどんな値であっても，Cとの論理和で必ず出力は1となります。このため，出力が1のところからは，AとBと出力との関係を確認することはできません。そこでCが0の箇所について注目してみます。

Cが0のときにA，Bがどうなっているかをみると，A，Bが両方とも0，片方が0のときは出力が0であり，A，Bの両方ともが1のときは，出力が1になっています。

これは単純に，A，Bの論理積 A \cdot B そのものの結果となっています。

以上より，この真理値表は

A \cdot B + C

と表現でき、答えは（5）となります。

以上3通りの方法で解いてみましたが，最も時間が掛からないのは方法3かと思います。問題の解き方としては，まずは真理値表を眺めてみて，力技でできそうかを考えてみる，すぐには思いつきそうになければ，方法1か方法2で法則通りに解いてみるというのが良さそうです。

方法1と方法2は法則通りに解いていけば必ず解答できますが，計算に時間が多少かかることと，途中で計算を間違えてしまうと余計に時間がかかってしまうのが欠点です。

解答

（5）