問題
次の文章は,回転界磁形三相同期発電機の無負荷誘導起電力に関する記述である。
回転磁束を担う回転子磁極の周速をv[m/s],磁束密度の瞬時値をb[T],磁束と直交する導体の長さをl[m]とすると,1本の導体に生じる誘導起電力e[V]は次式で表される。
e = vbl
極数をp,固定子内側の直径をD[m]とすると,極ピッチ\tau[m]は \tau = \dfrac{\pi D}{p} であるから, f [Hz]の起電力を生じる場合の周速vは v = 2 \tau f である。したがって,角周波数\omega [rad/s]を\omega = 2 \pi f として,上述の磁束密度瞬時値b[T]を b(t) = B_m sin \omega t と表した場合,導体1本あたりの誘導起電力の瞬時値e(t)は,
e(t) = E_m sin \omega t
E_m = \fbox{(ア)} B_m l
となる。
また,回転磁束の空間分布が正弦波でその最大値がB_mのとき,1極の磁束密度の \fbox{(イ)} B[T]は B = \dfrac{2}{\pi} B_m であるから,1極の磁束 \Phi [Wb]は\Phi = \dfrac{2}{\pi} B_m \tau l である。
したがって,1本の導体に生じる起電力の実効値は次のように表すことができる。
\dfrac{E_m}{\sqrt{2}}f \Phi = \dfrac{\pi}{\sqrt{2}}f \Phi = 2.22 f \Phi
よって,三相同期発電機の1相あたりの直列に接続された電機子巻線の巻数をNとすると,回転磁束の空間分布が正弦波の場合,1相あたりの誘導起電力(実効値)E [V]は,
E = \fbox{(ウ)} f \Phi N
となる。
さらに,電機子巻線には一般に短節巻と分布巻が採用されるので,これらを考慮した場合,1相あたりの誘導起電力Eは次のように表される。
E = \fbox{(ウ)} k_W f \Phi N
ここでk_Wを\fbox{(エ)} という。
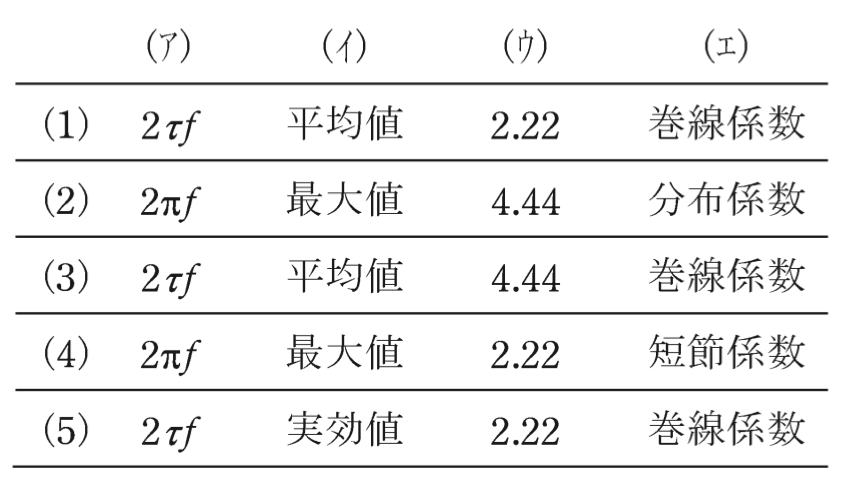
上記の記述中の空白箇所(ア)〜(エ)に当てはまる組み合わせとして,正しいものを次の(1)〜(5)のうちから一つ選べ。
解説
回転界磁形三相同期発電機とは,磁界を発生させるための界磁回路を回転させ,電気の発生する電機子回路が固定されたタイプの発電機です。界磁回路により発生した磁束が固定された電機子回路を横切ると,フレミングの右手の法則により電機子回路に起電力が生じます。発電機に負荷を接続しない状態で発生する電圧の大きさを,無負荷誘導起電力と言います。この無負荷誘導起電力に関する問題です。
(ア)
誘導起電力を求める式 e = vbl のvとbに,問題で与えられた式を代入をすることで解答が得られます。
問題文で,
e(t) = E_m sin \omega t
v = 2 \tau f
b(t) = B_m sin \omega t
と与えられていますので,これらを e = vbl の式に代入すると,
E_m sin \omega t = 2 \tau f ・ B_m sin \omega t ・ l
E_m = 2 \tau f ・ B_m ・ l
となりますので,解答は2 \tau fとなります。
周速が v = 2 \tau fとなる理由
問題文に
『極数をp,固定子内側の直径をD[m]とすると,極ピッチ\tau[m]は \tau = \dfrac{\pi D}{p} であるから, f [Hz]の起電力を生じる場合の周速vは v = 2 \tau f である。』
という記載がありますが,ここで書かれている内容が理解できなくても, v = 2 \tau f という結果を用いれば(ア)の解答を求めることができました。ここでは,周速度 v が 2 \tau f となる理由を少し丁寧に説明します。
vは下図のとおり,磁束が導体を横切る速度です。
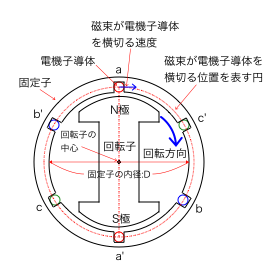
その速度の方向は,回転子の中心から磁束が導体を横切る位置までの距離を半径とする円の接線方向(上図でN極の上にある青色の矢印)で,大きさは単位時間あたりの円周上の移動距離です。
問題文で固定子の内径がDとして与えられていますので,これを回転子の中心から磁束が導体を横切る位置までの距離を半径とする円の直径と考えます。(上図のとおり,厳密には固定子の内面から電機子導体の中心までの長さを考慮する必要がありますが,その長さは小さいとして考えています。)
回転子の回転周波数をf_m[Hz](1秒間の回転数がf_m回)とすると,円周上のある1点は1秒間に円の円周の長さのf_m倍の距離を移動する(回転する)ことになるため,その速度(周速度)の大きさは,
v = \pi D f_m [m/s] ・・・式①
と求まります。
ここで,発生する交流電気の周波数と回転子の回転周波数との関係について考えます。
まずは極数が2極の場合についてです。
以下の図は,極数が2極の回転子が1回転するときに発電機のa相の電機子導体に発生する電圧の波形を時間t_1からt_4まで順に示したものです。a相の電機子導体は,発電機の図で赤色の丸で示しており,a,a'の2本1組で回路を構成しています。(同様にb相は青色,c相は緑色で示しています。)
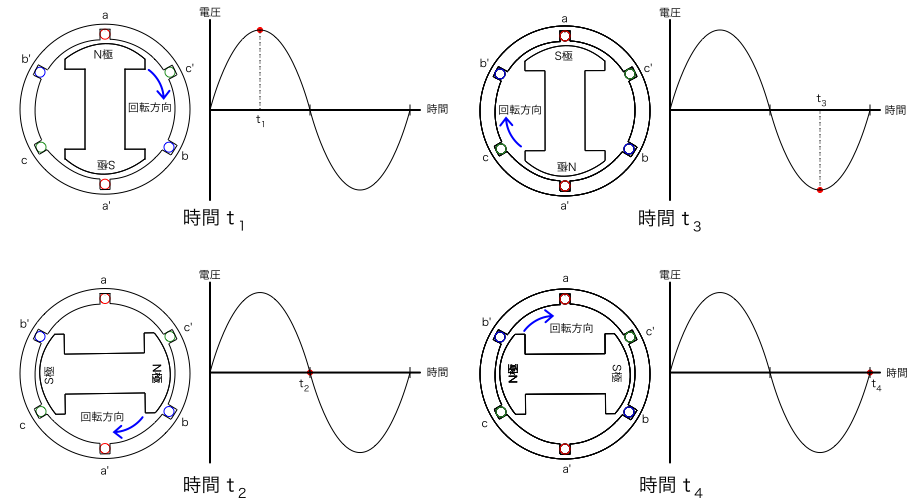
時間t_1では,磁極が電機子導体の真下の位置にあり,この位置では導体a,a'を横切る磁束の移動方向に垂直な磁束の成分の大きさが最大となるため,発生する電圧も最大となっています。(フレミングの右手の法則より,発生する電圧の大きさは導体の移動方向とそれに垂直な磁束の成分の大きさの積に比例するため。)
時間t_2では,磁極が電機子導体から最も離れた位置にあり,この位置では電機子導体a,a'を横切る磁束の移動方向と磁束の向きが同じ,すなわち導体を垂直方向に横切る磁束が0となるため,発生する電圧は0になっています。(フレミングの右手の法則から,導体の移動方向と磁束の向きが同じの場合,発生する電圧は0になるため。)
時間t_3では,時間t_1のときと同様に発生する電圧の大きさは最大ですが,磁極の極が時間t_1のときとは反対であるため,発生する電圧の極性も反対になっています。
時間t_4では,時間t_2と同様に磁極が電機子導体から最も離れた位置にあり,発生する電圧は0になっています。
以上のように極数が2の場合は,回転子が1回転すると発生する交流の電圧も1周期生じるので,回転子の回転周波数と発生する交流電気の周波数は同じとなります。
b相,c相についても位相が120°ずつ違うだけで同様です。
次にN極とS極が2組ある場合,すなわち極数が4極の場合の交流電気の周波数と回転子の周波数について考えます。2極の場合でみたとおり,1本の導体をN極,S極の磁界がそれぞれ1回ずつ導体を横切ると,1周期の交流電気が発生しました。
4極の場合は,下図のとおり,N極とS極の磁極の対が2組あり,電機子側の回路も2組(a相であれば,a1-a'1とa2-a'2の2組)あります。
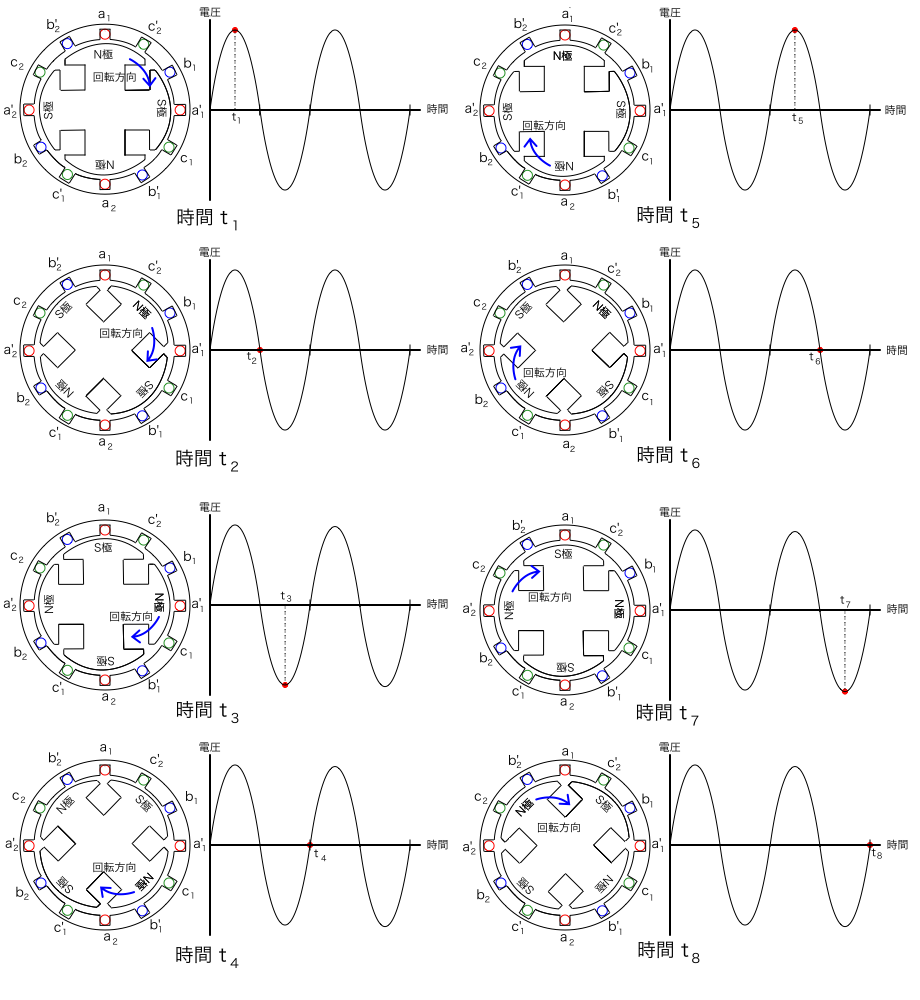
上図ではa相の電機子回路に発生する電圧の波形を時間毎に記載していますが,回転子が1回転する間に,1組のN極,S極の磁界はa1-a'1とa2-a'2の電機子回路を1回ずつ横切ることになるため,発生する交流電気の波形は2周期分となります。
時間t_1では,a1,a'1,a2,a'2の電機子導体を横切る磁束の移動方向と磁束の向きが垂直となる位置に磁極があるため,発生する電圧も最大となっています。
時間t_2では,電機子導体a1,a'1,a2,a'2を横切る磁束の移動方向と磁束の向きが同じ,すなわち導体を垂直方向に横切る磁束が0となる位置(a1-a'1とa2-a'2の導体間の中間の位置)に磁極が来ているため,発生する電圧は0になっています。
時間t_3では,時間t_1と同様に発生する電圧の大きさは最大となりますが,磁極の極性が時間t_1のときとは反対であるため,電圧の極性は反対となっています。
時間t_4では,時間t_2と同様に発生する電圧は0になります。
時間t_5では,再び磁極の位置が時間t_1のときと同様となるため,発生する電圧も再び最大になります。
この時点で1周期の交流電気が発生していますが,磁極はまだ半周目の位置にあります。
残りの半周も同様の動きですので,磁極が1回転したときには,2周期分の交流電気が発生することになります。
これは,回転子の回転周波数の2倍の周波数の交流が発生するということですので,回転子の回転周波数をf_m,発生する交流電気の周波数をfとすると,
f = 2f_m
という関係になります。
N極とS極を3組(極数が6極),4組(極数が8極)と増やした場合も同様に考えると,回転子が1回転するときに発生する交流電気の周波数は,それぞれの回転子の周波数の3倍,4倍となります。
したがって,極数をp極(N極とS極の対で考えると\dfrac{p}{2}対)とすると,回転子の回転周波数f_m,発生する交流電気の周波数fとの関係は以下のとおりとなります。
f = \dfrac{p}{2} f_m
ここまでで,発生する交流電気の周波数と回転子の回転周波数との関係が分かりました。
この結果を先ほど求めた磁束が導体を横切る速度vの式(式①)に代入すると,
v = \pi D f_m = \pi D \dfrac{2}{p} f_m [m/s] ・・・式②
となります。
あとは,この式を極ピッチ\tauを使って表現するだけです。
極ピッチとは,下図のようにN極とS極の軸の中心間の円周上の距離のことです。
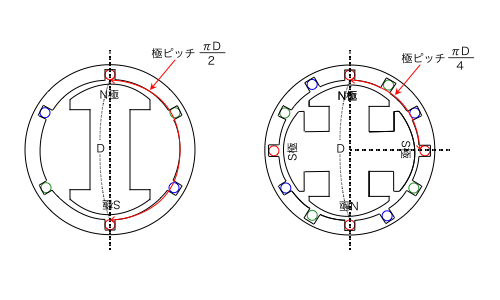
上図のとおり,2極の場合は円周の長さの半分,4極の場合は円周の長さの\dfrac{1}{4}が極ピッチになります。
p極の場合の極ピッチを\tauとすると,
\tau = \dfrac{\pi D}{p}
となるため,この式からDを求めると,
D = \dfrac{\tau p}{\pi}
となります。これを式②に代入すると,
v = \pi D \dfrac{2}{p} f_m = 2 \tau f
となります。
長くなりましたが,これでようやく f [Hz]の起電力を生じる場合の周速vを v = 2 \tau f と表すことができました。
最後にこれまでの内容を整理して書くと以下のとおりとなります。
- 回転子磁極の周速 v は,固定子の内径(直径)が D ,固定子の回転周波数が f_m のとき, v = \pi D f_m [m/s]となる。
- 回転子の回転周波数f_mと発生する交流電気の周波数fとの関係は,極数pとすると, f = \dfrac{p}{2} f_m となる。
- 極数がp極の場合の極ピッチ\tauは \tau = \dfrac{\pi D}{p}となる。
- これらの式より, f [Hz]の起電力を生じる場合の周速vは v = 2 \tau f と表すことができる。
(イ)
問題文にある B = \dfrac{2}{\pi} B_m の B_m は,正弦波で表される磁束密度の瞬時値 b(t) の最大値です。正弦波の最大値に \dfrac{2}{\pi} を掛けたものが B ですが,この問題では B が何と呼ばれているか問われています。
解答の選択肢を見ると,平均値,最大値,実効値が候補としてあげられていますが,最大値は先ほどの説明のとおり B_m であるため,最大値という解答は明らかに誤りです。解答は平均値か実効値のどちらかということになりますが,
・実効値は最大値に \dfrac{1}{\sqrt{2}} をかけたもの
・平均値は最大値に \dfrac{2}{\pi} をかけたもの
ということを知っていれば,解答は平均値であることが分かります。
正弦波の平均値,実効値の定義から計算で求めることも可能ですが,定義を理解した上で結果は覚えておいた方がよいかと思います。
(ウ)
同期発電機の電機子回路の導体1本に生じる起電力の実効値は, 2.22 f \Phi であると問題文で与えられていますが,電機子回路の巻き数をNにすると,起電力の実効値がどうなるかというのがこの問題です。
巻き数がNなので,単純に1本がN倍になると考えて, 2.22 f \Phi Nと解答したくなりますが,同期発電機の電機子回路の巻き数の数え方は,以下の図のように,N極側の導体とS極側の導体を1組として巻き数を数えます。(下図で右側の図は発電機を真横から見た図ですが,この図では電機子回路の巻き数は1回です。)
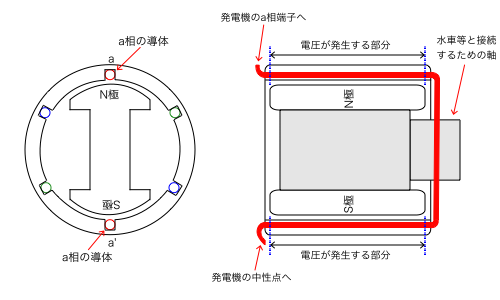
したがって,巻き数がNの場合の起電力は,1本の導体に生じる起電力の2N倍となり, 2 \times 2.22 f \Phi = 4.44 f \Phi となります。
(エ)
同期電動機の電機子巻線の巻き方は,下図のように各相毎の巻線をそれぞれ1カ所に集中して巻く集中巻と,固定子の円周上に分散させて巻く分布巻があります。通常は固定子の円周を広く活用できる分布巻が採用されています。
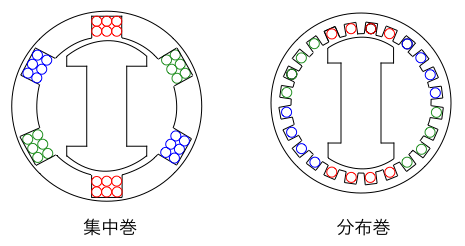
集中巻では,1本ずつの導体が同じ場所に集中して配置されているため,それぞれの導体を磁極による磁界が横切るタイミングが同じです。これらの導体をすべて直列に接続して発電機の端子電圧とした場合,その端子電圧は各導体に生じる電圧の大きさが同じであるため,単純に導体の本数の倍数の大きさになります。(厳密には,導体の大きさがあるため,全く同じ場所に集中して導体を巻くことはできないため,その分のずれは生じます。)
分布巻では1本ずつの導体が巻かれている位置が違うため,磁界がそれぞれの導体を横切るタイミングが異なります。このため,あるタイミングでは,誘導起電力が最大となっている導体や,これから最大値になろうとしている導体,あるいは既に最大値を超えて小さくなっている導体などがあり,これらの導体の直列接続として発電機の端子に現れる電圧の大きさは,集中巻と比べて小さくなります。
次に全節巻,単節巻についてです。
これまで説明で用いてきた発電機の図では,各相の巻線1組の対がそれぞれ磁極の中陣軸上の位置にくるように導体が巻かれていました。このように巻線は全節巻と呼ばれています。全節巻では,N極側の磁界が導体を横切るタイミングとS極側の磁界が導体を横切るタイミングが同じであるため,それぞれの導体に生じる誘導起電力の大きさは常に同じです。
一方で下図のように,磁極の中心軸から片方の巻線の巻く位置を少しずらした位置で巻く巻き方もあり,これを短節巻と言います。
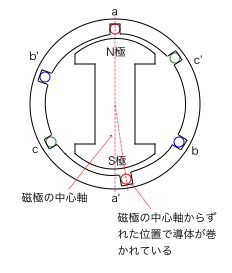
単節巻では,N極側の磁界が導体を横切るタイミングとS極側の磁界が導体を横切るタイミングが常に異なります。N極側の導体とS極側の導体も直列に接続されていますので,各導体に生じる電圧の合成として現れる発電機の端子電圧の大きさは,単節巻の方が全節巻と比べて小さくなります。
まとめると,分布巻,単節巻とすることにより,集中巻,全節巻の場合よりも誘導起電力の大きさが小さくなりますが,その割合を表した係数を巻線係数と言います。分布巻による割合を分布係数,単節巻による割合を単節係数といい,これらの積が巻線係数になっています。
解答
(3)