問題
電動機と負荷の特性を,回転速度を横軸,トルクを縦軸に描く,トルク対速度曲線で考える。電動機と負荷の二つの曲線が,どのように交わるかを見ると,その回転数における運転が,安定か不安定かを判定することができる。誤っているものを次の(1)〜(5)のうちから一つ選べ。
(1)負荷トルクよりも電動機トルクが大きいと回転は加速し,反対に電動機トルクよりも負荷トルクが大きいと回転は減速する。回転速度一定の運転を続けるには,負荷と電動機のトルクが一致する安定な動作点が必要である。
(2)巻線形誘導電動機では,回転速度の上昇とともにトルクが減少するように,二次抵抗を大きくし,大きな始動トルクを発生させることができる。この電動機に回転速度の上昇とともにトルクが増える負荷を接続すると,両曲線の交点が安定な動作点となる。
(3)電源電圧を一定に保った直流分巻電動機は,回転速度の上昇とともにトルクが減少する。一方,送風機のトルクは,回転速度の上昇とともにトルクが増大する。したがって,直流分巻電動機は,安定に送風機を駆動することができる。
(4)かご形誘導電動機は,回転トルクが小さい時点から回転速度を上昇させるとともにトルクが増大,最大トルクを越えるとトルクが減少する。この電動機に回転速度でトルクが変化しない定トルク負荷を接続すると,電動機と負荷のトルク曲線が2点で交わる場合がある。この場合,加速時と減速時によって安定な動作点が変わる。
(5)かご形誘導電動機は,最大トルクの速度より高速な領域では回転速度の上昇とともにトルクが減少する。一方,送風機のトルクは,回転速度の上昇とともにトルクが増大する。したがって,かご形誘導電動機は,安定に送風機を駆動することができる。
解説
(1)
負荷トルク,すなわちある物を回転させるために必要なトルクよりも,電動機側のトルクの方が大きければ,その差のトルクを常に加え続けることになります。トルクが加わるとは,回転するための力を加え続けることですので,その回転速度はどんどんと速くなります。反対に物を回転させるために必要なトルクの方が電動機のトルクよりも大きければ,その物を回転させるための力が足らないということなので,回線速度はどんどんと遅くなります。
電動機と負荷のトルクが一致していれば,トルクがバランスしていることになるため,回転速度は変化せずにある一定の速度で回転を続けることができます。
したがって,この問題文の記述は正しいです。
(2)
この文章が正しかどうかを判断するためには,誘導電動機のトルクとすべりの関係を表すグラフをイメージできる必要があります。
横軸をすべり,縦軸をトルクとして誘導電動機の特性をグラフで表すと以下の図の様になります。
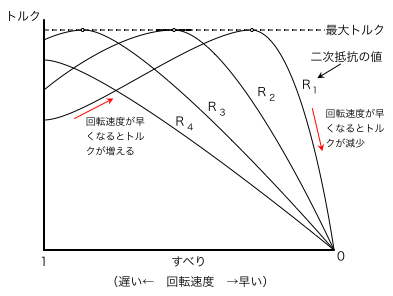
横軸はすべりですので,グラフの右側,すべりが0に近づくにつれて回転速度が速くなり,左側のすべりが1に近づくほど,回転速度は遅くなります。
グラフには複数の線を記載していますが,二次抵抗の値をR1,R2,R3,R4と増やしていったときのトルクとすべりの関係をそれぞれ表しています。
このグラフを見ながら,問題文の「回転速度の上昇とともにトルクが減少するように,二次抵抗を大きくし,大きな始動トルクを発生させることができる」という箇所について考えます。
まず「回転速度の上昇とともにトルクが減少するように,二次抵抗を大きくし」という箇所についてです。回転速度の上昇,すなわちすべりが0に近づく(横軸で右側にいく)につれてトルクが減少するには,グラフは右肩下がりの形状になっている必要があります。上記グラフを見ると,二次抵抗が大きくなるほど,最大トルクが発生すべりが1の方に移動しており,その結果グラフが右肩下がりになる範囲が増えていっているのが分かります。
このことから,この文章は正しいと考えられます。
つぎに後半部分の「二次抵抗を大きくし,大きな始動トルクを発生させることができる」という箇所です。始動トルクとは,回転数が0,すなわちすべりが1のときのトルクのことであり,グラフでは横軸の一番左端のときのトルクが該当します。
二次抵抗の値ごとの始動トルクを見ると,二次抵抗が大きくしていくと,始動トルクの大きさもだんだん大きくなっていますが,ある値以上になると,今度は始動トルクが小さくなる傾向があります。例えば上記グラフで二次抵抗がR3よりも大きいR4のときの始動トルクは,R3のときの始動トルクと比べ小さくなっています。
したがって,「二次抵抗を大きくし,大きな始動トルクを発生させることができる」というのは必ずしもそうならない場合もありそうですが,二次抵抗を大きくしすぎない範囲では正しいと言えますので,一般的な説明としては正しいと考えてよいのかと思います。
「回転速度の上昇とともにトルクが減少する」特性がある範囲で電動機を運転させ,「回転速度の上昇とともにトルクが増える負荷を接続」すれば,下記グラフのように電動機と負荷の特性を表す二つの曲線の交点が運転点となります。
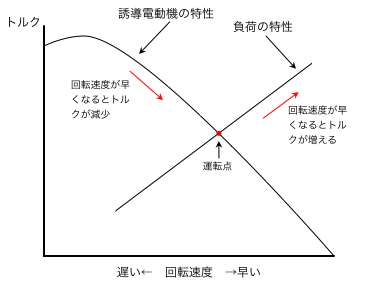
この運転点では,電動機が何らかの理由で加速して回転速度が速くなるとトルクは減少しますが,電動機に接続されている負荷のトルクは増えるため,電動機のトルクの方が小さくなります。負荷のトルクよりも小さなトルクで負荷を回転させることはできないため,電動機の回転速度は減速しますが,回転速度が遅くなると電動機のトルクは大きくなり,負荷のトルクは小さくなります。それぞれのトルクの大きさが再び同じ大きさになると,電動機と負荷のトルクがバランスして運転を継続することができます。
反対に電動機が何らかの理由で減速して回転速度が遅くなると,電動機のトルクは増加しますが,負荷のトルクは減少します。その結果,電動機のトルクの方が負荷のトルクよりも大きくなり,そのトルクの差で電動機の回転速度が増加します。電動機の回転速度が増加すると,電動機のトルクは減少し,負荷のトルクは増えるため,それぞれのトルクの大きさが再び同じ大きさになると,電動機と負荷のトルクがバランスして運転を継続することができます。
したがって,この文章の記述は正しいと言えます。
(3)
問題文前半の「電源電圧を一定に保った直流分巻電動機は,回転速度の上昇とともにトルクが減少する」は,直流分巻電動機の特性についてですが,これが正しいのかどうか確認をします。
直流分巻電動機の等価回路は以下の図のように表すことができます。
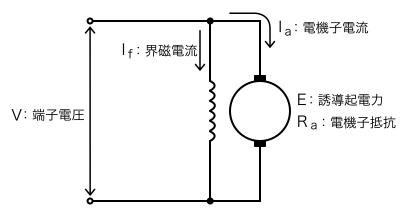
直流電動機のトルクの大きさは,フレミングの左手の法則より,電機子電流の大きさと磁極の磁束の大きさに比例します。直流電動機のトルクの大きさを T ,電機子電流を I_a ,磁極の磁束を \Phi ,比例定数を k_1 とすると,
T = k_1 I_a \Phi
と表すことができます。
この式だけですと,回転速度とトルクとの関係がよく分かりません。回転数が変わると何が変わるのかということを考えたとき,上図の等価回路では,電機子回路で生じる誘導起電力の大きさです。
電機子回路に生じる誘導起電力の大きさは,フレミングの右手の法則より,電動機の回転速度,磁極の磁束の大きさに比例します。誘導起電力の大きさをE,電動機の回転速度をn,比例定数を k_2 とすると,
E = k_2 \Phi n
と表すことができます。
この式より,電動機の回転速度が速くなると誘導起電力の大きさが大きくなり,回転速度が遅くなると誘導起電力の大きさも小さくなることが分かります。
回転速度と誘導起電力との関係はこれでわかりましたが,トルクを表す式には誘導起電力の大きさが含まれていません。そこで誘導起電力が変化すると次に何が変化するかを考えてみると,上図の等価回路で電動機の端子電圧が一定であるため,電機子電流の大きさが変わります。
等価回路より
V = E + R_a I_a
という関係があるため,電機子電流の大きさは
I_a = \dfrac{V - E}{R_a}
となります。この式より, E が大きくなると,電機子電流は小さくなることが分かります。
ここまでで,電動機の回転数が上昇すると,誘導起電力の大きさが大きくなり,その結果電機子電流が小さくなることが分かりました。
ここでトルクを表す式を見てみると,トルクは電機子電流の大きさに比例しているため,電機子電流が小さくなるとトルクの大きさも小さくなることになります。
したがって問題文の「電源電圧を一定に保った直流分巻電動機は,回転速度の上昇とともにトルクが減少する」というのは正しいことになります。
続いて,「送風機のトルクは回転速度の上昇とともにトルクが増大する」という負荷特性の記述についてです。
この文章が正しいかどうかを判断するためには,ある回転速度で回転している送風機の回転速度を上昇させたときに,上昇する前と後とで,送風機を回転させるためのトルクの大きさがどのように変化するかを考える必要があります。
送風機は風を送るために電動機で羽根を回転させていますが,空気はその羽根の面に押されることで移動しています。回転速度を上昇させると,空気は速い速度で羽根に押されることになるため,それだけ空気の移動速度も速くなり,時間当たりに送風できる空気の量が多くなります。そのため,それを維持するために必要な羽根を回転させる力,すなわちトルクの大きさは,回転速度を上昇する前のトルクよりも大きいというのはイメージとしては正しそうです。
送風機の回転速度とトルクとの関係が具体的にどうなるのか,以下の送風機の模式図を使ってもう少し考えます。

送風機の羽根の回転により送風される空気は,ある速度で移動しますので,運動エネルギーを持っています。この空気が移動するエネルギーを求めることで,そこからそのエネルギーを与えるために必要な力,トルクを求めます。
上図のように断面積がA[m2]の筒を速度v[m/s]で空気が移動しているとして,このときの空気の運動エネルギーを求めます。
断面積A[m2]の筒を速度v[m/s]で通過する空気の時間当たりの体積は、
Av [m3/s]
です。空気の密度を\rho[kg/m3]とすると、時間当たり(1秒)に筒を通過する空気の質量は
\rho Av [kg/s]
となります。したがってこの移動する空気が持つ時間当たりの運動エネルギーは
\dfrac{1}{2}(\rho Av)v^2 = \dfrac{1}{2}\rho Av^3 [W] ・・・式①
となります。時間当たりの運動エネルギーの単位は[J/s],すなわち[W]となります。
送風機の羽根の回転により空気は移動しているため,この運動エネルギーのもとは送風機を回転させている電動機の出力です。実際は電動機の出力がそのまま全て空気の運動エネルギーに変わるということはなく,筒と空気との摩擦や風の乱れなどによるエネルギーの損失があり,電動機の出力の方が空気の運動エネルギーよりも大きくなりますが,ここでは簡単に考えるためにそれらの損失は無視して,電動機の出力がそのまますべて空気の運動エネルギーになると考えます。
電動機の出力P[W]は,送風機の羽根の回転角速度を\omega[rad/s],トルクをT[Nm]とすると,
P = \omega T ・・・式②
と表されます。
空気の移動速度は羽根の回転速度に比例するため,その比例定数をkとすると,空気の移動速度vは
v = k \omega
と表されます。
これを式①に代入して,空気の時間当たりの運動エネルギー[W]を表す式を\omega を使って表現すると,
\dfrac{1}{2}\rho Av^3 = \dfrac{1}{2}\rho Ak^3 \omega ^3
となります。これが式②で表される電動機の出力と等しいので,
\dfrac{1}{2}\rho Ak^3 \omega ^3 = \omega T
T = \dfrac{1}{2}\rho Ak^3 \omega ^2
となります。この式より,送風機を回転させるために必要なトルクは回転数の2乗に比例するということが分かります。したがって「送風機のトルクは回転速度の上昇とともにトルクが増大する」というのは正しいことが分かりました。
最後に「直流分巻電動機は,安定に送風機を駆動することができる」という記述についてです。
最初に確認したとおり,「電源電圧を一定に保った直流分巻電動機は,回転速度の上昇とともにトルクが減少する」という特性があり,「送風機のトルクは回転速度の上昇とともにトルクが増大」することも確認できました。これらのトルクと回転速度との関係をグラフに表すと以下のとおりとなり,問題文(2)と同様に電動機は安定して運転が可能となります。
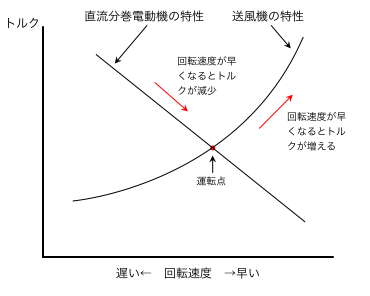
したがって,この問題文の記述は正しいです。
(4)
まずは「かご形誘導電動機は,回転トルクが小さい時点から回転速度を上昇させるとともにトルクが増大,最大トルクを越えるとトルクが減少する」という記述についてです。かご形でも巻線形でも,問題(2)で示した誘導電動機のトルクと回転速度(すべり)との関係を表す曲線の基本的な形状は変わりませんので,この曲線でこの記述が正しいかどうかを判断しますが,この曲線の特性は記述のとおりとなっていることが分かります。
続いて,「この電動機に回転速度でトルクが変化しない定トルク負荷を接続すると,電動機と負荷のトルク曲線が2点で交わる場合がある。この場合,加速時と減速時によって安定な動作点が変わる。」という後半の部分について考えます。
「回転速度でトルクが変化しない定トルク負荷」の特性を表す線と,電動機の特性を表す曲線を一緒に記載すると下図のようになります。
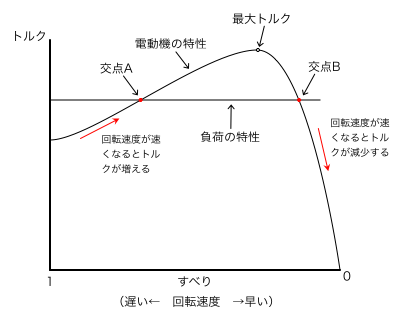
上図のとおり,負荷の特性を表す線と電動機の特性を表す線は2点(交点Aと交点B)で交わります。負荷の特性を表す線が電動機の最大トルクと等しい点でのみ交わる場合も考えられますが,問題文でも全てのケースで2点で交わるということではないことを表現するため,「電動機と負荷のトルク曲線が2点で交わる場合がある。」と記載されています。したがって,「この電動機に回転速度でトルクが変化しない定トルク負荷を接続すると,電動機と負荷のトルク曲線が2点で交わる場合がある。」
という記載は正しいです。
残りは「この場合,加速時と減速時によって安定な動作点が変わる」という記述についてです。
上図の交点Aで運転しているときに,電動機が加速した場合を考えて見ます。
交点Aでは,電動機は回転速度が速くなるとトルクも増える特性があります。電動機が何らかの理由で加速して回転速度が速くなると,トルクも増えていきますが,電動機に接続されている負荷のトルクは変わらないため,電動機のトルクの方が大きくなります。負荷のトルクよりも大きなトルクで負荷を回転させると,そのトルクの差で電動機はさらに加速していきます。
反対に電動機が何らかの理由で減速して回転速度が遅くなると,トルクは減少します。この場合は,電動機のトルクの方が負荷のトルクよりも小さくなり,負荷を回転させるためのトルクが足りなくなるため,負荷を回転させることができず,どんどん減速して最終的には停止してしまいます。
したがって,交点Aでは電動機は安定して運転することができません。
交点Bではどうか考えてみます。交点Bでは,電動機は回転速度が速くなるとトルクが減少する特性があります。電動機が何らかの理由で加速して回転速度が速くなるとトルクは減少しますが,電動機に接続されている負荷のトルクは変わらないため,電動機のトルクの方が小さくなります。負荷のトルクよりも小さなトルクで負荷を回転させることはできないため,電動機の回転速度は減速しますが,回転速度が遅くなると電動機のトルクは大きくなります。そのトルクの大きさが再び負荷のトルクと同じ大きさになると,電動機と負荷のトルクがバランスして運転を継続することができます。
反対に電動機が何らかの理由で減速して回転速度が遅くなると,トルクは増加します。この場合は,電動機のトルクの方が負荷のトルクよりも大きくなり,そのトルクの差で電動機の回転速度が増加します。電動機の回転速度が増加すると,電動機のトルクは減少するため,そのトルクの大きさが再び負荷のトルクと同じ大きさになると,電動機と負荷のトルクがバランスして運転を継続することができます。
したがって,交点Bでは電動機は安定して運転することが可能です。
以上より,電動機の加速,減速に関わらず,交点Aのある最大トルクから左側の領域(回転速度が上昇するとトルクが大きくなる領域)では安定して運転することができず,交点Bのある最大トルクから右側の領域(回転速度が上昇するとトルクが小さくなる領域)では安定して運転することが可能であるため,問題文の「この場合,加速時と減速時によって安定な動作点が変わる」という記載は誤りです。
よって(4)の問題文は誤りとなります。
(5)
かご形誘導電動機の特性については,問題(4)で説明したとおりであり,最大トルクの速度より高速な領域では回転速度の上昇とともにトルクが減少します。また,送風機の特性については,問題(3)で説明したとおり,回転速度の上昇とともにトルクが増大します。
かご形誘導電動機と送風機の特性を表す曲線をまとめて記載すると下図のとおりとなります。

上図で示す電動機と負荷の特性を表す曲線が交わる点で電動機を運転すれば,これまでの問題で説明したとおり,電動機は安定して運転を継続することができます。
したがって,この問題文の記載は正しいです。
解答
(4)