問題
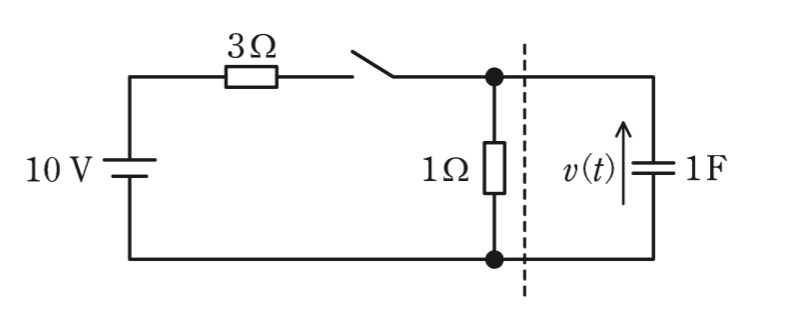
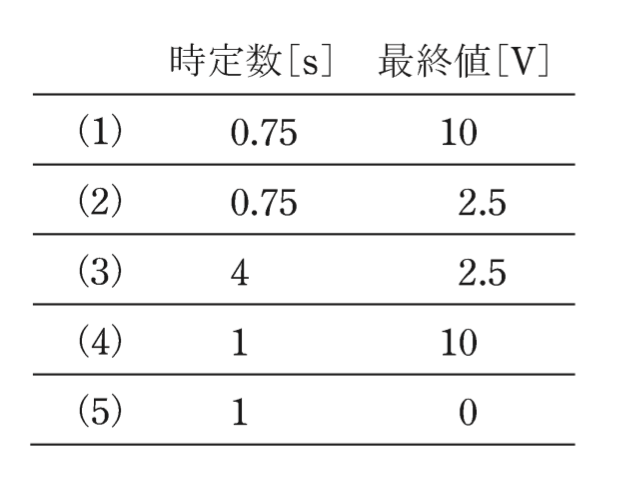
図の回路のスイッチを閉じたあとの電圧v(t)の波形を考える。破線から左側にテブナンの定理を適用することで，回路の時定数[s]とv(t)の最終値[V]の組合せとして，最も近いものを次の（1）〜（5）のうちから一つ選べ。
ただし，初めスイッチは開いており，回路は定常状態にあったとする。
解説
過渡現象に関しての問題です。過渡現象については，こちらで説明をしていますので，必要に応じてご確認下さい。問題では，回路の時定数とコンデンサの電圧の最終値がどうなるかについて問われていますので，それぞれについて別々に求めていきます。
コンデンサの電圧の最終値
これは過渡現象が完了したあとの回路の状態を考えることですぐに求まります。
回路のスイッチを閉じると回路には電流が流れますが，最初のうちは，1Ωの抵抗，コンデンサの両方に電流が流れます。コンデンサに流れる電流は，コンデンサの容量いっぱいまで電荷が蓄えられるとそれ以降は電流が流れることができないため，以下の図のとおり電流は抵抗にのみ流れるようになります。
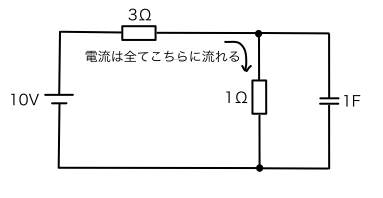コンデンサと1Ωの抵抗は並列に接続されているため，上図の状態のときのコンデンサの両端の電圧は，1Ωの抵抗にかかる電圧と同じとなります。1Ωの抵抗にかかる電圧は，3Ωの抵抗との分圧となるため，その大きさは
\dfrac{1}{1+3} \times 10 = \dfrac{10}{4} = 2.5 [V]
となります。この電圧値がコンデンサの電圧の最終値です。
時定数
時定数を求めるために，まずは問題文に記載されているとおり，破線から左側をテブナンの定理を用いて電源と抵抗のみの回路に書き換えます。破線から左側の回路を見たときのインピーダンスは，3Ωの抵抗と1Ωの抵抗の並列接続となるため，その大きさは
\dfrac{3 \times 1}{3+1}=\dfrac{3}{4}[Ω]
となり，破線から左側の回路の開放電圧は10Vであるため，問題の回路は以下のとおり変換できます。
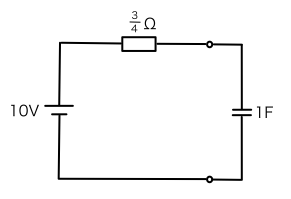
問題の回路は，抵抗とコンデンサが直列に接続された回路に変換できましたが，抵抗とコンデンサが直列に接続された回路の時定数T[s]は，抵抗値をR[Ω]，コンデンサの静電容量をC[F]とすると，T=RCであるため，
T=\dfrac{3}{4} \times 1 = 0.75 [s]
となります。
抵抗とコンデンサが直列に接続された回路の時定数がRCとなることについては，こちらで解説しています。
解答
（2）
