問題
図のように，線間電圧（実効値）200Vの対称三相交流電源に，1台の単相電力計W_1，X=4Ωの誘導性リアクタンス3個，R=9Ωの抵抗3個を接続した回路がある。単相電力計W_1の電流コイルはa相に接続し，電圧コイルはb-c相間に接続され，指示は正の値を示していた。この回路について，次の（a）及び（b）の問に答えよ。
ただし，対称三相交流電源の相順は，a，b，cとし，単相電力計W_1
の損失は無視できるものとする。
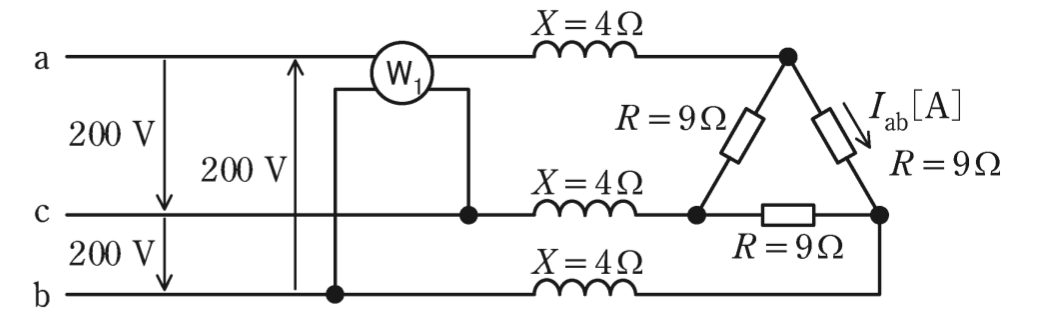
（a）R=9Ωの抵抗に流れる電流I_{ab}の実効値[A]として，最も近いものを次の（1）〜（5）のうちから一つ選べ。
（1）6.77 （2）13.3 （3）17.3 （4）23.1 （5）40.0
（b）単相電力計W_1の指示値[kW]として，最も近いものを次の（1）〜（5）のうちから一つ選べ。
（1）0 （2）2.77 （3）3.70 （4）4.80 （5）6.40
解説
問題の回路を見ると，インダクタンス，抵抗の大きさは各相で同じであるため，この問題は不平衡回路の問題ではなく，三相平衡回路として考えることができます。
（a）
抵抗に流れる電流を求める問題です。三相平衡回路であるため，1相のみを考えて抵抗に流れる電流を求めていきたいですが，抵抗が接続された回路はΔ接続となっているため，このままでは1相のみを考えることができません。このため，まずは抵抗が含まれるΔ回路をY回路に変換して，1相のみの計算を行えるようにします。ここで得られる電流値はa相に流れる線電流となりますが，求めるべき抵抗に流れる電流は相間の電流値であるため，そのままでは答えにはなりません。そのため，線電流値を相電流値に変換する必要があります。線電流をI_線 ，相電流をI_相とすると，線電流と相電流との間には，I_相 = \dfrac{1}{\sqrt{3}}I_線という関係があるため，これを用いて相電流値を求めることができます。以下順を追って答えを求めていきます。
step
1抵抗回路のΔ-Y変換
Δ接続時のa相とb相の間のインピーダンスをZ_{ab} ，b相とc相の間のインピーダンスをZ_{bc} ，c相とa相の間のインピーダンスをZ_{ca} とし，Y接続時のa相，b相，c相のインピーダンスをそれぞれ順にZ_{a} ，Z_{b} ，Z_{c} とすると，Y接続時のa相のインピーダンスは，Δ-Y変換の公式より，以下のとおり求めることができます。
Z_{a}=\dfrac{Z_{ab} Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}
問題の回路では，Z_{ab}=Z_{bc}=Z_{ca}=9[Ω]であるため，これを上記の式に代入すると，
Z_{a}=\dfrac{9 \cdot 9}{9+9+9}=3[Ω]
と求まります。
step
2線電流値を求める
線電流を求めるためには，相電圧が必要ですが，問題の回路では，相間の電圧値が記載されているため，まずはこれを相電圧値に変換します。1相のみの計算としてa相を選定し，a相の電圧を\dot V_{a}とすると，
\dot V_{a}=\dfrac{200}{\sqrt{3}}[V]
となります。
a相に接続されているのは，4[Ω]のリアクタンスと先ほど求めたZ_{a}=3の抵抗のみであるため，a相の線電流を\dot I_a[A]とすると，
\dot I_{a} = \dfrac{\dot V_a}{R+jX} = \dfrac{200}{\sqrt{3} (3+j4)} [A]
となります。なお， \dot V_{a} はベクトル表記でありながら，虚数部の数値が含まれておりませんが，これは \dot V_{a} を位相の基準（ \dot V_{a} の方向が0°）としているためです。
step
3線電流値を相電流に変換
求まった線電流を最初に述べた，I_相 = \dfrac{1}{\sqrt{3}}I_線の関係を使って，相電流を求めます。求める相電流は \dot I_{ab}ですが，大きさだけ考えると\dot I_aの大きさを\sqrt{3}で割るだけです。\dot I_aの大きさ I_a は，
I_a = \left| \dfrac{200}{\sqrt{3} (3+j4)} \right| = \dfrac{200}{\sqrt{3} \sqrt{3^2+4^2}} = \dfrac{40}{\sqrt{3}}
であるので，
I_{ab} = \dfrac{1}{\sqrt{3}}I_a = \dfrac{1}{\sqrt{3}} \dfrac{40}{\sqrt{3}} \fallingdotseq 13.3
となり，答えは（2）となります。
（b）
問題の単相電力計が取り込んでいる電圧は，b相，c相間の相電圧 V_{bc} ，a相の線電流 I_a ですので，この電力計が示す有効電力 P は， V_{bc} と I_a の位相差を \theta とすると，
P=V_{bc} I_a cos \theta
で求めることが可能です。 V_{bc} は問題の図から， I_a は問題(a)の回答からすぐに求めることが可能ですが， cos \theta の値は \dot V_{bc} と \dot I_a の位相関係が分からないと求めることができません。このためベクトル図を書いて， \dot V_{bc} と \dot I_a の位相関係がどのようになっているかを調べます。
\dot I_a は問題(a)において，
\dot I_{a}=\dfrac{200}{\sqrt{3} (3+j4)}
と求まっています。 \dot I_a は \dot V_a を位相の基準として求めていますので， \dot V_a と \dot I_a の位相関係をベクトル図で書くと以下のようになります。（電圧，電流ともに大きさは正確ではありません。）
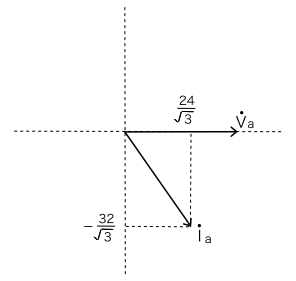
このベクトル図において，\dot I_{a} の実軸，虚軸方向の成分の大きさを記載していますが，それらは以下の計算で求めています。
\dot I_{a}=\dfrac{200}{\sqrt{3} (3+j4)} = \dfrac{200 (3-j4)}{\sqrt{3} (3+j4)(3-j4)}
= \dfrac{200 (3-j4)}{\sqrt{3} (9+14)} = \dfrac{8}{\sqrt{3}} (3-j4) = \dfrac{24}{\sqrt{3}}-j \dfrac{32}{\sqrt{3}}
次に \dot V_a と \dot V_{bc} の位相関係についてですが， \dot V_{bc} は相電圧 \dot V_{b} と相電圧 \dot V_{c} との間の線間電圧ですので，以下のベクトル図のとおり， \dot V_a よりも90°遅れた位相になっています。
\dot V_a を基準として， \dot V_{bc} と \dot I_a のベクトル図を一緒に書くと以下のとおりになります。（この図でも，電圧，電流ともに大きさは正確ではありません。）
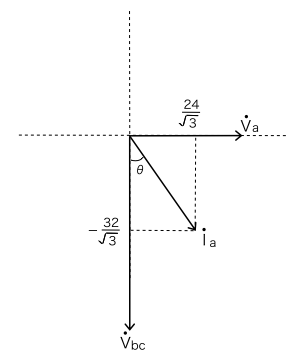さきに述べたとおり， \dot V_{bc} と \dot I_a の位相差を \theta としていますので，こちらも図に反映しています。ここまで来ればあと一息です。求めるべき有効電力 Pは， P=V_{bc} I_a cos \theta でした。この式が意味するところは，有効電力 Pは電圧の位相と電流の位相が同位相の成分の積が有効電力となるということなので， I_a cos \theta というのは， \dot I_a の成分のうち， V_{bc} と同じ方向の成分を選ぶ必要があります。 V_{bc} は虚軸上に乗っているため， I_aの虚軸方向の成分が V_{bc} の方向と同じになります。その大きさは，上記ベクトル図から，
I_a cos \theta = \dfrac{32}{\sqrt{3}}
であり， \dot V_{bc} の大きさは問題の図より200であるので，求めるべき有効電力は
P=V_{bc} I_a cos \theta = 200 \dfrac{32}{\sqrt{3}} \fallingdotseq 3695 (W) \fallingdotseq 3.70 (kW)
となり，答えは（3）となります。
別解
上記の求め方はベクトル図を描いて有効電力を求める方法ですので，直感的には理解しやすいですが，ベクトル図を書く時間が必要であったり，仮に電圧が V_{bc} ではなく， V_{ab} であったりすると，これと同じ方向の電流成分を求めるのが大変になります。ここでは，ベクトル図を書かずに，計算で一度に有効電力と無効電力を計算する方法を紹介します。この方法は電験2種以上の問題では必須の計算方法です。
交流の電圧ベクトルを\dot E，電流ベクトルを\dot I，電流ベクトルの共役複素数を \overline{\dot I} ，有効電力をP，無効電力をQとしたとき，以下の計算にてP，Qを求めることができます。
\dot{E} \overline{\dot I} = P+jQ
\dot{E} \cdot \overline{\dot I} を計算した結果の実数部分がP，虚数部分がQとなりますので，
P = Re \{ \dot{E} \overline{\dot I} \}
Q = Im \{ \dot{E} \overline{\dot I} \}
と表記することもあります。
早速この式を使って問題を解いていきます。この問題では，電圧，電流は以下のとおりでした。
\dot V_{bc} = -j200
\dot I_{a}=\dfrac{200}{\sqrt{3} (3+j4)} = \dfrac{24}{\sqrt{3}}-j \dfrac{32}{\sqrt{3}}
これを先ほどの計算方法で計算すると，
\dot V_{bc} \overline{\dot I_{a}} = j200 \left( \dfrac{24}{\sqrt{3}}-j \dfrac{32}{\sqrt{3}} \right)
= -j \dfrac{4800}{\sqrt{3}} + j \dfrac{6400}{\sqrt{3}} \fallingdotseq 3695 - j2771
となります。
この計算結果の実数部分が有効電力ですので，
P = 3695 [W] \fallingdotseq 3.70 [kW]
となり，最初の解き方と同じ結果が得られました。
解答
（a）（2）
（b）（3）
