問題
図のように,三つの抵抗R_1=3\Omega,R_2=6\Omega,R_3=2\Omegaと電圧V[V]の直流電源からなる回路がある。抵抗R_1,R_2,R_3の消費電力をそれぞれP_1[W],P_2[W],P_3[W]とするとき,その大きさの大きい順として,正しいものを次の(1)〜(5)のうちから一つ選べ。
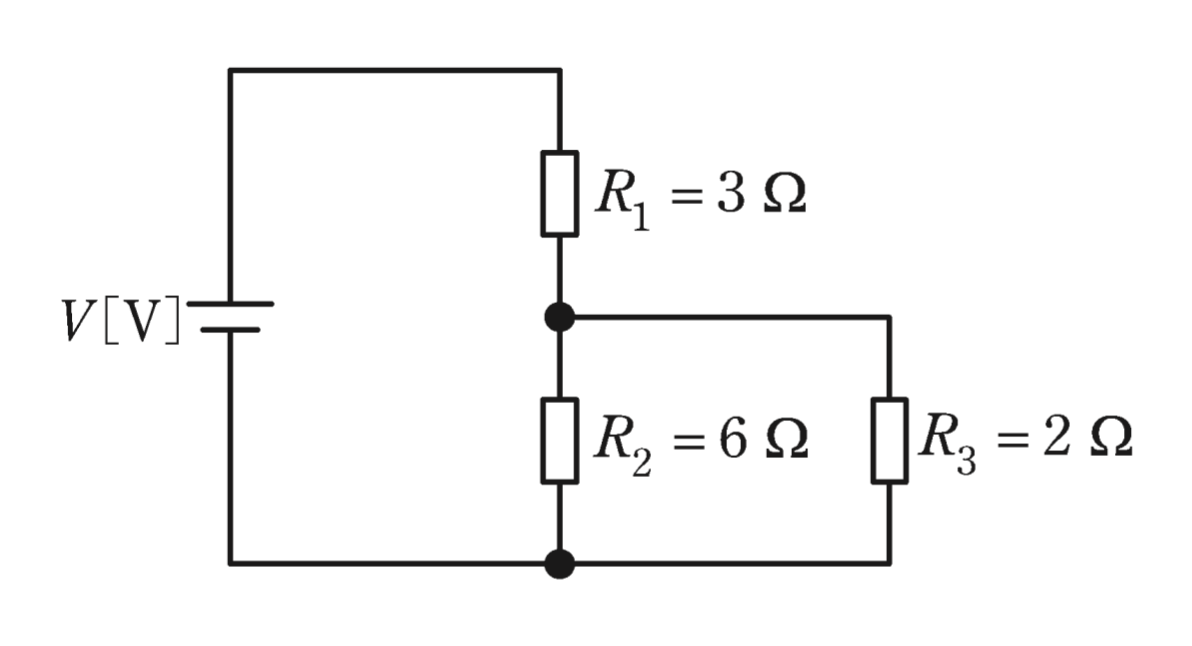
(1) P_1 > P_2 > P_3 (2) P_1 > P_3 > P_2 (3) P_2 > P_1 > P_3
(4) P_2 > P_3 > P_1 (5) P_3 > P_1 > P_2
解説
抵抗R[Ω]で消費する電力P[W}は,抵抗に流れる電流をI[A]とすると,
P=I^2R
となります。このまま,各抵抗に流れる電流を求め,各抵抗で消費する電力を求めてもよいですが,消費電力の式を抵抗にかかる電圧をEとして,電圧と抵抗で表した式にすると,I=\frac{E}{R}であるので,
P=I^2R=(\dfrac{E}{R})^2 \cdot R=\dfrac{E^2}{R}
となります。この式を用いて,各抵抗で消費する電力を求めていきます。
step
1各抵抗にかかる電圧
R_2とR_3の並列接続部分にかかる電圧を求めるには,並列部分の合成抵抗値を求める必要があります。R_2とR_3の合成抵抗値は,
\dfrac{R_2 \cdot R_3}{R_2+R_3}=\dfrac{6 \cdot 2}{6+2}=\dfrac{12}{8}=1.5
であるので,R_1にかかる電圧をE_1,R_2とR_3の並列接続部分にかかる電圧をE_pとすると,
E_1=V \times \dfrac{3}{3+1.5}=\dfrac{V}{1.5}
E_p=V \times \dfrac{1.5}{3+1.5}=\dfrac{V}{3}
となります。
step
2各抵抗での消費電力
各抵抗での消費電力をP_1,P_2,P_3とすると,
P_1=\dfrac{{E_1}^2}{R_1}=\dfrac{V^2}{1.5^2 \cdot 3}=\dfrac{V^2}{6.75}
P_2=\dfrac{{E_p}^2}{R_2}=\dfrac{V^2}{3^2 \cdot 6}=\dfrac{V^2}{54}
P_3=\dfrac{{E_p}^2}{R_3}=\dfrac{V^2}{3^2 \cdot 2}=\dfrac{V^2}{18}
となり,上記の消費電力の大きさを比較すると,
P_1 > P_3 >P_2
となります。
解答
(2)